Análisis de Brotes y Modelamiento en Salud Pública: Todo en Una Sola Página

Content from Día 2 – Taller modelos compartimentales: Construyendo un modelo matemático simple para Zika.

Last updated on 2024-03-12 | Edit this page

Overview

Questions

¿Cómo construir un modelo simplificado de zika?

Objectives

Al final de este taller usted podrá:

Aplicar conceptos como parámetros, $R_0$ e inmunidad de rebaño, aprendidos en la sesión A del taller
Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
Realizar un modelo simple en R para una enfermedad transmitida por vector
Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección

1. Introducción

En este taller usted aplicará los conceptos básicos del modelamiento de Enfermedades Transmitidas por Vectores (ETV) mediante el uso del lenguaje R con énfasis en el funcionamiento de los métodos, utilizando como ejemplo un modelo básico de infección por un arbovirus: el virus del Zika.

2. Agenda

Parte 1: 9:00 am a 10:30 am - Instrucciones (5 mins) - Lectura del taller (10 mins) - Desarrollo taller Zika Parte B (45 mins con acompañamiento de monitores) - Revisión grupal del código (10 mins) - Revisión de resultados (20 mins) Descanso: 10:30 am a 11:00 am Parte 2: 11:00 am - 1:00 pm - Simular intervenciones (30 mins) - Revisión de las intervenciones (30 mins) - Discusión final (60 mins)

3. Conceptos básicos a desarrollar

En esta práctica se desarrollarán los siguientes conceptos:

Modelo SIR para ETV Zika
Parametrización de un modelo dinámico
Evaluación de un modelo dinámico
Parametrización de intervenciones de control (fumigación, mosquiteros y vacunación) para una ETV

4. Paquetes requeridos

Cargue los paquetes necesarios ingresando en R los siguientes comandos:

R

library(deSolve)   # Paquete deSolve para resolver las ecuaciones diferenciales
library(tidyverse) # Paquetes ggplot2 y dplyr de tidyverse
library(cowplot) # Paquete gridExtra para unir gráficos.

Si desea puede tomar notas en el script de R, para esto se recomienda usar el símbolo de comentario # después de cada línea de código (ver ejemplo arriba). O podría utilizar un archivo Rmd para tener un aspecto similar al del taller.

5. Compartimentos del modelo básico de Zika

$S_h$ : Humanos susceptibles
$I_h$ : Humanos infecciosos
$R_h$ : Humanos recuperados de la infección (inmunizados frente a nueva infección)
$S_v$ : Vectores susceptibles
$E_v$ : Vectores expuestos
$I_v$ : Vectores infecciosos

6. Parámetros del modelo

Ahora se usarán los parámetros que discutimos en la parte A del taller. Si aún no los tiene, estos se pueden encontrar en la guía de aprendizaje de la parte A del taller.

Desafío 1

Busque los valores de los parámetros del modelo y diligéncielos en el recuadro de abajo. Tenga en cuenta que todos los parámetros usados tienen la misma unidad de tiempo (días).

R

Lv       <-        # Esperanza de vida de los mosquitos (en días)
Lh       <-        # Esperanza de vida de los humanos (en días)
PIh      <-        # Periodo infeccioso en humanos (en días)
PIv      <-        # Periodo infeccioso en vectores (en días)
PEI      <-        # Período extrínseco de incubación en mosquitos adultos (en días)
muv      <-        # Tasa per capita de mortalidad del vector (1/Lv)
muh      <-        # Tasa per capita de mortalidad del hospedador (1/Lh)
alphav   <-        # Tasa per capita de natalidad del vector
alphah   <-        # Tasa per capita de natalidad del hospedador
gamma    <-        # Tasa de recuperación en humanos (1/PIh)
delta    <-        # Tasa extrínseca de incubación (1/PEI)
ph       <-        # Probabilidad de transmisión del vector al hospedador dada una picadura por un mosquito infeccioso a un humano susceptible
pv       <-        # Probabilidad de transmisión del hospedador al vector dada una picadura por un mosquito susceptible a un humano infeccioso
Nh       <-        # Número de humanos
m        <-        # Densidad de mosquitos hembra por humano
Nv       <-        # Número de vectores (m * Nh)
R0       <-        # Número reproductivo básico
b        <-        sqrt((R0 * muv*(muv+delta) * (muh+gamma)) /
                   (m * ph * pv * delta)) # Tasa de picadura
betah    <-        # Coeficiente de transmisión del mosquito al humano
betav    <-        # Coeficiente de transmisión del humano al mosquito
TIME     <-        # Número de años que se va a simular

7. Ecuaciones del modelo

Para este modelo emplearemos las siguientes ecuaciones diferenciales:

7.1 Humanos

\[\ \frac{dSh}{dt} = \alpha_h N_h - \beta_h \frac {I_v}{N_h}S_h - \mu_h S_h \]

\[\ \frac{dIh}{dt} = \beta_h \frac {I_v}{N_h}S_h - (\gamma + \mu_h) I_h \]

\[\ \frac{dRh}{dt} = \gamma I_h - \mu_h R_h\]

7.2 Vectores

\[\ \frac{dSv}{dt} = \alpha_v N_v - \beta_v \frac{ I_h} {N_h}S_v - \mu_v Sv\]

\[\ \frac{dE_v}{dt} = \beta_v \frac{I_h} {N_h}S_v- (\delta + \mu_v) Ev\]

\[\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v\]

8. Fórmula para calcular $R_0$ (Número reproductivo básico)

Fórmula necesaria para estimar $R_0$:

\[ R_0 = \frac{mb^2 p_h p_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma)} \]

9. Modelo en R

Es hora de implementar el modelo en R. Para lograrlo, usaremos la función ode del paquete desolve. Para el ejercicio se emplearán 4 argumentos de la función esta función: el primero son las condiciones iniciales del modelo (argumento y); el segundo es la secuencia temporal donde se ejecutará el modelo (argumento times); el tercero es una función que contiene las ecuaciones diferenciales que entrarán al sistema (argumento fun); por último un vector que contiene los parámetros con los que se calculará el sistema (argumento parms).

R

# NO la copie a R sólo tiene fines ilustrativos.
ode(y      = # Condiciones iniciales,
    times  = # Tiempo,
    fun    = # Modelo o función que lo contenga,
    parms  = # Parámetros
)

Desafío 2

En esta sección se empezará por crear la función (argumento fun), para ello es necesario traducir las ecuaciones del modelo a R. Abajo encontrará la función ya construida, por favor reemplace los parámetros faltantes (Cambie PAR por los parámetro correspondientes) en las ecuaciones:

R

arbovmodel <- function(t, x, params) {
  
  Sh <- x[1]    # Humanos susceptibles
  Ih <- x[2]    # Humanos infecciosos 
  Rh <- x[3]    # Humanos recuperados
  Sv <- x[4]    # Vectores susceptibles
  Ev <- x[5]    # Vectores expuestos
  Iv <- x[6]    # Vectores infecciosos
  
  with(as.list(params), # entorno local para evaluar derivados
       {
         # Humanos
         dSh   <-  PAR * Nh - PAR * (Iv/Nh) * Sh - PAR * Sh   
         dIh   <-  PAR * (Iv/Nh) * Sh - (PAR + PAR) * Ih
         dRh   <-  PAR * Ih  - PAR * Rh
         
         # Vectores
         dSv  <-  alphav * Nv - PAR * (Ih/Nh) * Sv - PAR * Sv 
         dEv  <-  PAR * (Ih/Nh) * Sv - (PAR + PAR)* Ev
         dIv  <-  PAR * Ev - PAR * Iv
         
         dx   <- c(dSh, dIh, dRh, dSv, dEv, dIv)
         list(dx)
       }
  )
}

10. Resuelva el Sistema

En esta sección se crearán los tres argumentos faltantes para usar la función ode y se creará un objeto de clase data.frame con los resultados de la función ode. Por favor complete y comente el código para:

Los VALORES de las condiciones iniciales del sistema.
Los ARGUMENTOS de la función ode en el paquete deSolve.

Desafío 3

R

# Secuencia temporal (times)
times  <- seq(1, 365 * TIME , by = 1)
# Los parámetros (parms)
params <- c(
  muv      = muv,     
  muh      = muh, 
  alphav   = alphav,
  alphah   = alphah,
  gamma    = gamma,   
  delta    = delta,   
  betav    = betav,       
  betah    = betah,   
  Nh       = Nh,      
  Nv       = Nv
)
# Condiciones iniciales del sistema (y)
xstart <- c(Sh = VALOR?,        # COMPLETE Y COMENTE
            Ih = VALOR?,        # COMPLETE Y COMENTE
            Rh = VALOR?,        # COMPLETE Y COMENTE
            Sv = VALOR?,        # COMPLETE Y COMENTE
            Ev = VALOR?,        # COMPLETE Y COMENTE
            Iv = VALOR?)        # COMPLETE Y COMENTE
# Resuelva las ecuaciones
out <- as.data.frame(ode(y      = ARGUMENTO?,   # COMPLETE Y COMENTE
                         times  = ARGUMENTO?,   # COMPLETE Y COMENTE
                         fun    = ARGUMENTO?,   # COMPLETE Y COMENTE
                         parms  = ARGUMENTO?))  # COMPLETE Y COMENTE

11. Resultados

Desafío 4

Para tener una visualización más significativa de los resultados, convierta las unidades de tiempo de días a años y a semanas.

R

# Cree las opciones de tiempo para años y semanas 
out$years <- 
out$weeks <-

Observe el comportamiento del modelo en distintas escalas de tiempo (semanas y años):

11.1 Comportamiento General (Población humana)

R

# Revise el comportamiento general del modelo para 100 años
p1h <- ggplot(data = out, aes(y = (Rh + Ih + Sh), x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población humana total') +
  theme_bw() + ylab('Número') + xlab('Años')
p2h <- ggplot(data = out, aes(y = Sh, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Número') + xlab('Años')
p3h <- ggplot(data = out, aes(y = Ih, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Número') + xlab('Años')
p4h <- ggplot(data = out, aes(y = Rh, x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1h, p2h, p3h, p4h, ncol = 2)

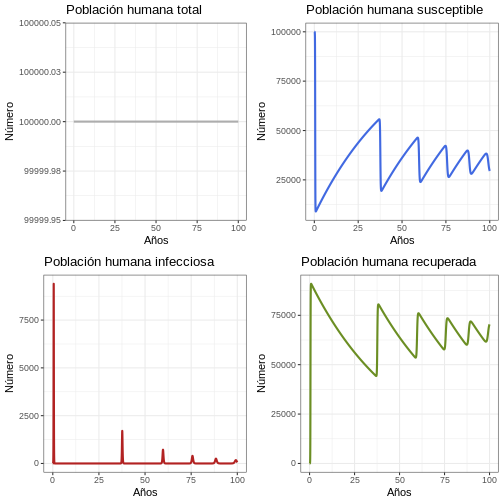
11.2 Comportamiento General (Población de vectores)

R

# Revise el comportamiento general del modelo
p1v <- ggplot(data = out, aes(y = (Sv + Ev + Iv), x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población total de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p2v <- ggplot(data = out, aes(y = Sv, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población susceptible de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p3v <- ggplot(data = out, aes(y = Ev, x = years)) +
  geom_line(color = 'orchid', size = 1) +
  ggtitle('Población expuesta de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
p4v <- ggplot(data = out, aes(y = Iv, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población infecciosa de mosquitos') +
  theme_bw() + ylab('Número') + xlab('Años')
plot_grid(p1v, p2v, p3v, p4v, ncol = 2)

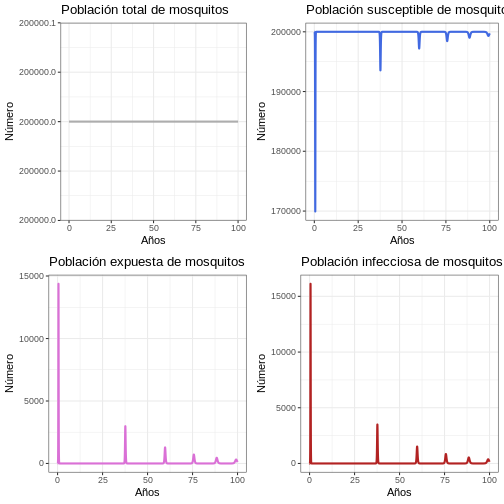
11.3 Proporción

Por favor dé una mirada más cuidadosa a las proporciones y discútalas

R

p1 <- ggplot(data = out, aes(y = Sh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p2 <- ggplot(data = out, aes(y = Ih/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infecciosa') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
p3 <- ggplot(data = out, aes(y = Rh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Proporción') + xlab('Años') +
  coord_cartesian(ylim = c(0,1))
plot_grid(p1, p2, p3, ncol = 2)

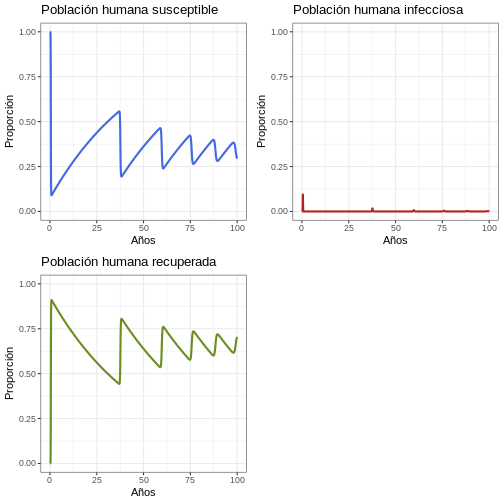
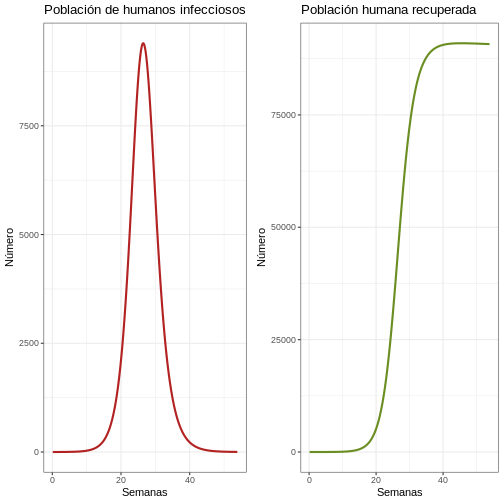
11.4 La primera epidemia

R

# Revise la primera epidemia
dat <- out %>% filter(weeks < 54)
p1e <- ggplot(dat, aes(y = Ih, x = weeks)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población de humanos infecciosos') +
  theme_bw() + ylab('Número') + xlab('Semanas')
p2e <- ggplot(dat, aes(y = Rh, x = weeks)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('Número') + xlab('Semanas')
plot_grid(p1e, p2e)

11.5 Algunos aspectos por discutir

¿Qué tan sensible es el modelo a cambios en el $R_0$?
¿Qué razones hay (según el modelo) para el intervalo de tiempo entre estas epidemias simuladas?
¿Cómo se puede calcular la tasa de ataque?

11.6 Modele una o más intervenciones de control

Ahora, utilizando este modelo básico, modelar por grupos el impacto de las siguientes intervenciones:

Grupo 1. Fumigación contra mosquitos
Grupo 2. Mosquiteros/angeos
Grupo 3. Vacunación que previene frente a infecciones

Para cada intervención:

Indique en qué parte del modelo haría los cambios.
De acuerdo a la literatura que explique estas intervenciones y describa cómo parametrizará el modelo. ¿Todas estas intervenciones son viables en la actualidad?

Puntos clave

Revise si al final de esta lección adquirió estas competencias:

Aplicar conceptos como parámetros, $R_0$ e inmunidad de rebaño, aprendidos en la sesión A del taller
Traducir fórmulas matemáticas de las interacciones entre los parámetros del modelo a código de R
Realizar un modelo simple en R para una enfermedad transmitida por vector
Discutir cambios en las proyecciones del modelo cuando se instauran diferentes estrategias de control de la infección

Sobre este documento

Contribuciones

Zulma Cucunuba & Pierre Nouvellet: Versión inicial
Kelly Charinga & Zhian N. Kamvar: Edición
José M. Velasco-España: Traducción de Inglés a Español y Edición
Andree Valle-Campos: Ediciones menores

Contribuciones son bienvenidas vía pull requests. El archivo fuente del documento original puede ser encontrado aquí.

Asuntos legales

Licencia: CC-BY Copyright: Zulma Cucunuba & Pierre Nouvellet, 2017

Referencias

de Carvalho, S. S., Rodovalho, C. M., Gaviraghi, A., Mota, M. B. S., Jablonka, W., Rocha-Santos, C., Nunes, R. D., Sá-Guimarães, T. da E., Oliveira, D. S., Melo, A. C. A., Moreira, M. F., Fampa, P., Oliveira, M. F., da Silva-Neto, M. A. C., Mesquita, R. D., & Atella, G. C. (2021). Aedes aegypti post-emergence transcriptome: Unveiling the molecular basis for the hematophagic and gonotrophic capacitation. PLoS Neglected Tropical Diseases, 15(1), 1–32. https://doi.org/10.1371/journal.pntd.0008915

Chang, C., Ortiz, K., Ansari, A., & Gershwin, M. E. (2016). The Zika outbreak of the 21st century. Journal of Autoimmunity, 68, 1–13. https://doi.org/10.1016/j.jaut.2016.02.006

Cori, A., Ferguson, N. M., Fraser, C., & Cauchemez, S. (2013). A new framework and software to estimate time-varying reproduction numbers during epidemics. American Journal of Epidemiology, 178(9), 1505–1512. https://doi.org/10.1093/aje/kwt133

Duffy, M. R., Chen, T.-H., Hancock, W. T., Powers, A. M., Kool, J. L., Lanciotti, R. S., Pretrick, M., Marfel, M., Holzbauer, S., Dubray, C., Guillaumot, L., Griggs, A., Bel, M., Lambert, A. J., Laven, J., Kosoy, O., Panella, A., Biggerstaff, B. J., Fischer, M., & Hayes, E. B. (2009). Zika Virus Outbreak on Yap Island, Federated States of Micronesia. New England Journal of Medicine, 360(24), 2536–2543. https://doi.org/10.1056/nejmoa0805715

Ferguson, N. M., Cucunubá, Z. M., Dorigatti, I., Nedjati-Gilani, G. L., Donnelly, C. A., Basáñez, M. G., Nouvellet, P., & Lessler, J. (2016). Countering the Zika epidemic in Latin America. Science, 353(6297). https://doi.org/10.1126/science.aag0219

Heesterbeek, J. A. P. (2002). A brief history of R0 and a recipe for its calculation. Acta Biotheoretica, 50(3). https://doi.org/10.1023/A:1016599411804

Lee, E. K., Liu, Y., & Pietz, F. H. (2016). A Compartmental Model for Zika Virus with Dynamic Human and Vector Populations. AMIA … Annual Symposium Proceedings. AMIA Symposium, 2016, 743–752.

Pettersson, J. H. O., Eldholm, V., Seligman, S. J., Lundkvist, Å., Falconar, A. K., Gaunt, M. W., Musso, D., Nougairède, A., Charrel, R., Gould, E. A., & de Lamballerie, X. (2016). How did zika virus emerge in the Pacific Islands and Latin America? MBio, 7(5). https://doi.org/10.1128/mBio.01239-16

Content from Día 3 - Taller Introducción a la analítica de brotes

Last updated on 2024-03-12 | Edit this page

Overview

Questions

¿Cómo modelar y analizar un brote?

Objectives

Al final de este taller usted podrá:

Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.

Tiempos de ejecución

Explicación del taller (10 minutos)

Realización del taller (100 minutos taller)

Parte 1: Estructura de datos y CFR (15 min)
Parte 2: Incidencia y tasa de crecimiento (45 min)
Parte 3: Rt (40 min)

Discusión 30 minutos

Introducción

Un nuevo brote de virus del Ébola (EVE) en un país ficticio de África occidental

Conceptos básicos a desarrollar

En esta práctica se desarrollarán los siguientes conceptos:

Transmisión de enfermedades infecciosas de persona a persona
Número de reproducción básico
Número de reproducción instantáneo
Probabilidad de muerte (IFR, CFR)
Intervalo serial
Tasa de crecimiento
Incidencia

1. Estructura de datos

Preparación previa

Antes de comenzar, descargue la carpeta con los datos y el proyecto desde Carpetas de datos . Ahí mismo encontrará un archivo .R para instalar las dependencias necesarias para este taller.

Recuerde abrir el archivo RProject denominado Taller-Brotes-Ebola.Rproj antes de empezar a trabajar. Este paso no solo le ayudará a cumplir con las buenas prácticas de programación en R, sino también a mantener un directorio organizado, permitiendo un desarrollo exitoso del taller.

Cargue de librerías:

Cargue las librerías necesarias para el análisis epidemiológico. Los datos serán manipulados con tidyverse que es una colección de paquetes para la ciencia de datos.

R

library(tidyverse) # contiene ggplot2, dplyr, tidyr, readr, purrr, tibble
library(readxl) # para leer archivos Excel
library(binom) # para intervalos de confianza binomiales
library(knitr) # para crear tablas bonitas con kable()
library(incidence) # para calcular incidencia y ajustar modelos
library(EpiEstim) # para estimar R(t)

Cargue de bases de datos

Se le ha proporcionado la siguiente base de datos:

casos: una base de datos de casos que contiene información de casos hasta el 1 de julio de 2014.

Para leer en R este archivo, utilice la función read_rds de tidyverse. Se creará una tabla de datos almacenada como objeto de clase tibble.

R

casos <- read_rds("data/casos.rds")

Estructura de los datos

Explore la estructura de los datos. Para esto puede utilizar la función glimpse de tidyverse, la cual nos proporciona una visión rápida y legible de la estructura interna de nuestro conjunto de datos.

R

glimpse(casos)

OUTPUT

Rows: 166
Columns: 11
$ id_caso                  <chr> "d1fafd", "53371b", "f5c3d8", "6c286a", "0f58…
$ generacion               <dbl> 0, 1, 1, 2, 2, 0, 3, 3, 2, 3, 4, 3, 4, 2, 4, …
$ fecha_de_infeccion       <date> NA, 2014-04-09, 2014-04-18, NA, 2014-04-22, …
$ fecha_inicio_sintomas    <date> 2014-04-07, 2014-04-15, 2014-04-21, 2014-04-…
$ fecha_de_hospitalizacion <date> 2014-04-17, 2014-04-20, 2014-04-25, 2014-04-…
$ fecha_desenlace          <date> 2014-04-19, NA, 2014-04-30, 2014-05-07, 2014…
$ desenlace                <chr> NA, NA, "Recuperacion", "Muerte", "Recuperaci…
$ genero                   <fct> f, m, f, f, f, f, f, f, m, m, f, f, f, f, f, …
$ hospital                 <fct> Military Hospital, Connaught Hospital, other,…
$ longitud                 <dbl> -13.21799, -13.21491, -13.22804, -13.23112, -…
$ latitud                  <dbl> 8.473514, 8.464927, 8.483356, 8.464776, 8.452…

Como puede observar contactos tiene 11 columnas (variables) y 166 filas de datos. En un rápido vistazo puede observar el tipo de las variables por ejemplo, la columna desenlace tiene formato carácter (chr) y contiene entre sus valores "Recuperación" o "Muerte".

Además, puede encontrar estas variables:

El identificador id_caso
La generación de infectados (cuantas infecciones secundarias desde la fuente hasta el sujeto han ocurrido)
La fecha de infección
La fecha de inicio de síntomas
La fecha de hospitalización
La fecha del desenlace que, como se puede observar, en la siguiente variable puede tener entre sus opciones NA (no hay información hasta ese momento o no hay registro), recuperación y muerte
La variable género que puede ser f de femenino o m de masculino
El lugar de hospitalización, en la variable hospital
Y las variables longitud y latitud

Note que las fechas ya están en formato fecha (date).

2. CFR

Probabilidad de muerte en los casos reportados (`CFR`, por Case Fatality Ratio)

R

table(casos$desenlace, useNA = "ifany")

OUTPUT


      Muerte Recuperacion         <NA> 
          60           43           63

Desafío 1

Calcule la probabilidad de muerte en los casos reportados (CFR) tomando el número de muertes y el número de casos con desenlace final conocido del objeto casos. Esta vez se calculará el CFR con el método Naive. Los cálculos Naive (inocentes) tienen el problema de que pueden presentar sesgos, por lo que no deberían ser utilizados para informar decisiones de salud pública.

Durante este taller se le presentarán algunos retos, para los cuales obtendrá algunas pistas, por ejemplo en el presente reto se le presenta una pista, la cual es un fragmento del código que usted debe completar para alcanzar la solución. En los espacios donde dice COMPLETE por favor diligencie el código faltante.

R

muertes <-  COMPLETE

casos_desenlace_final_conocido <- sum(casos$desenlace %in% c("Muerte", "Recuperacion")) 

CFR <- COMPLETE / COMPLETE

Ejemplo,

R

# Reto
muertes <-  COMPLETE
#Solución
muertes <- sum(casos$desenlace %in% "Muerte")

OUTPUT

[1] 0.5825243

Para complementar el calculo del CFR se pueden calcular sus intervalos de confianza por medio de la función binom.confint. La función binom.confint se utiliza para calcular intervalos de confianza para una proporción en una distribución binomial, que corresponde, por ejemplo, a cuando tenemos el total de infecciones con desenlace final conocido (recuperado o muerte). Esta función pide tres argumentos: 1) el número de muertes y 2) el número total de casos con desenlace final conocido, es decir sin importar que hayan muerto o se hayan recuperado, pero sin cuenta los datos con NA; 3) el método que se utilizará para calcular los intervalos de confianza, en este caso “exact” (método Clopper-Pearson).

Desafío 2

Determine el CFR con sus intervalos de confianza utilizando la función binom.confint. Y obtenga este resultado:

**CFR con intervalos de confianza**
method	x	n	mean	lower	upper
exact	60	103	0.5825243	0.4812264	0.6789504

Pista

Recuerde diligenciar los espacios donde dice COMPLETE. Y obtenga este resultado

R

CFR_con_CI <- binom.confint(COMPLETE, COMPLETE, method = "COMPLETE") %>%
  kable(caption = "**COMPLETE ¿QUE TITULO LE PONDRÍA?**")

CFR_con_CI

3. Incidencia

3.1. Curva de incidencia diaria

El paquete incidence es de gran utilidad para el análisis epidemiológico de datos de incidencia de enfermedades infecciosas, dado que permite calcular la incidencia a partir del intervalo temporal suministrado (e.g. diario o semanal). Dentro de este paquete esta la función incidence la cual cuenta con los siguientes argumentos:

dates contiene una variable con fechas que representan cuándo ocurrieron eventos individuales, como por ejemplo la fecha de inicio de los síntomas de una enfermedad en un conjunto de pacientes.
interval es un intervalo de tiempo fijo por el que se quiere calcular la incidencia. Por ejemplo, interval = 365 para un año. Si no se especifica, el valor por defecto es diario.
last_date fecha donde se establecerá un limite temporal para los datos. Por ejemplo, la última fecha de hospitalización. Para este tercer argumento, podemos incluir la opción max y la opción na.rm. La primera para obtener la última fecha de una variable y la segunda para ignorar los NA en caso de que existan.

Por ejemplo, se podría escribir last_date = max(base_de_datos$vector_ultima_fecha, na.rm = TRUE)

Con esta información la función agrupa los casos según el intervalo de tiempo especificado y cuenta el número de eventos (como casos de enfermedad) que ocurrieron dentro de cada intervalo.

Desafío 3

Calcule la incidencia diaria usando únicamente el primer argumento de la función incidence ¿Qué fecha sería la más adecuada? Tenga en cuenta que se espera que esta sea la que pueda dar mejor información, es decir la menor cantidad de NAs.

R

incidencia_diaria <- incidence(COMPLETE)
incidencia_diaria

El resultado es un objeto de clase incidencia (incidence) que contiene el recuento de casos para cada intervalo de tiempo, lo que facilita su visualización y análisis posterior. Como puede observar la función produjo los siguientes datos:

OUTPUT

<incidence object>
[166 cases from days 2014-04-07 to 2014-06-29]

$counts: matrix with 84 rows and 1 columns
$n: 166 cases in total
$dates: 84 dates marking the left-side of bins
$interval: 1 day
$timespan: 84 days
$cumulative: FALSE

Como resultado de la función se produjo un objeto tipo lista. Este objeto arroja estos datos: 166 casos contemplados entre los días 2014-04-07 al 2014-06-29 para un total de 84 días; se menciona que el intervalo es de 1 día, dado que no se utilizo específico explicitamente el parámetro por lo cual quedó su valor por defecto. Finalmente se menciona “cumulative : FALSE” lo que quiere decir que no se esta haciendo el acumulado de la incidencia, es decir que los casos corresponden a los del intervalo interval: 1 day, es decir a los casos nuevos cada día en específico.

Ahora haga una gráfica de la incidencia diaria.

R

plot(incidencia_diaria, border = "black")

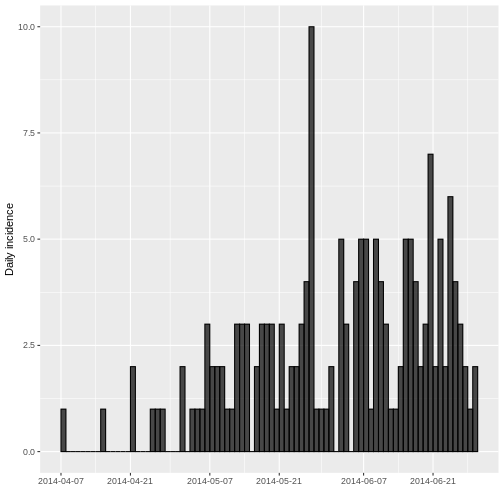
En el Eje X (Fechas): Se puede observar fechas van desde el 7 de abril de 2014 hasta una fecha posterior al 21 de junio de 2014. Estas fechas representan el período de observación del brote.

En el Eje Y (Incidencia Diaria): La altura de las barras indica el número de nuevos casos reportados cada fecha según el tipo de fecha escogido.

Dado que no se agregó el parámetro interval la incidencia quedó por defecto diaria, produciéndose un histograma en el que cada barra representa la incidencia de un día, es decir, los casos nuevos. Los días sin barras sugieren que no hubo casos nuevos para esa fecha o que los datos podrían no estar disponibles para esos días.

A pesar de que hay una curva creciente, hay periodos con pocos o ningún caso. ¿Porque cree que podrían darse estos periodos de pocos a pesar de la curva creciente?

3.2. Cálculo de la incidencia semanal

Teniendo en cuenta lo aprendido con respecto a la incidencia diaria, cree una variable para incidencia semanal. Luego, interprete el resultado y haga una gráfica. Para escoger la fecha que utilizará como última fecha debe asignarle un valor al argumento last_date de la función incidence ¿Qué fecha sería la más adecuada? Tenga en cuenta que la fecha debe ser posterior a la fecha que se haya escogido como el primer argumento.

Desafío 4

R

incidencia_semanal <- incidence(PRIMER ARGUMENTO,  #COMPLETE
                                SEGUNDO ARGUMENTO, #COMPLETE 
                                TERCER ARGUMENTO)  #COMPLETE

OUTPUT

<incidence object>
[166 cases from days 2014-04-07 to 2014-06-30]
[166 cases from ISO weeks 2014-W15 to 2014-W27]

$counts: matrix with 13 rows and 1 columns
$n: 166 cases in total
$dates: 13 dates marking the left-side of bins
$interval: 7 days
$timespan: 85 days
$cumulative: FALSE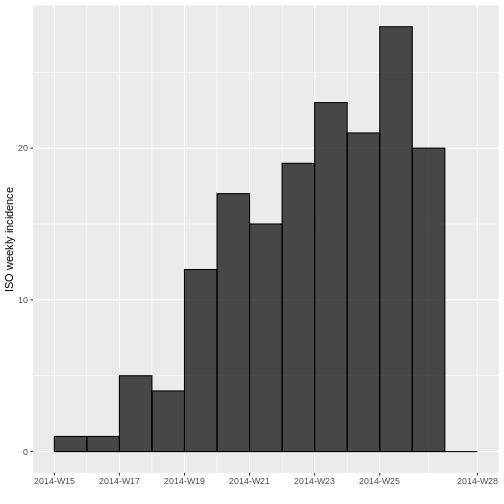

Compare la gráfica de incidencia diaria con la de incidencia semanal. ¿Qué observa? ¿Los datos se comportan diferente? ¿Es lo que esperaba? ¿Logra observar alguna tendencia?

4. Tasa de crecimiento

4.1. Modelo log-lineal

Estimación de la tasa de crecimiento mediante un modelo log-lineal

Para observar mejor las tendencias de crecimiento en el número de casos se puede visualizar la incidencia semanal en una escala logarítmica. Esto es particularmente útil para identificar patrones exponenciales en los datos.

Grafique la incidencia transformada logarítmicamente:

R

ggplot(as.data.frame(incidencia_semanal)) + 
  geom_point(aes(x = dates, y = log(counts))) + 
  scale_x_incidence(incidencia_semanal) +
  xlab("Semana") +
  ylab("Incidencia semanal logarítmica") + 
  theme_minimal()

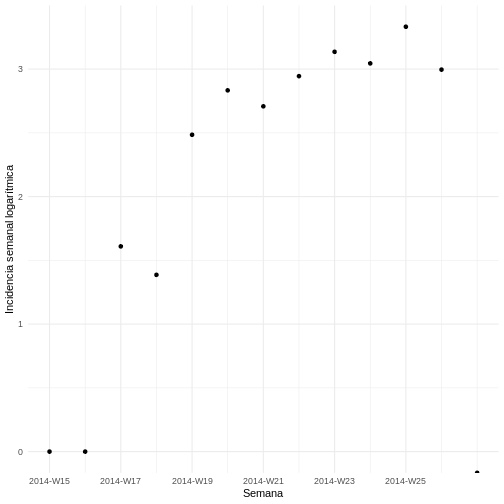
Ajuste un modelo log-lineal a los datos de incidencia semanal

R

ajuste_modelo <- incidence::fit(incidencia_semanal)
ajuste_modelo

OUTPUT

<incidence_fit object>

$model: regression of log-incidence over time

$info: list containing the following items:
  $r (daily growth rate):
[1] 0.04145251

  $r.conf (confidence interval):
          2.5 %     97.5 %
[1,] 0.02582225 0.05708276

  $doubling (doubling time in days):
[1] 16.72148

  $doubling.conf (confidence interval):
        2.5 %   97.5 %
[1,] 12.14285 26.84302

  $pred: data.frame of incidence predictions (12 rows, 5 columns)

Desafío 5

¿Qué observa en este resultado?

Solución

$model: Indica que se ha realizado una regresión logarítmica de la incidencia en función del tiempo. Esto implica que la relación entre el tiempo y la incidencia de la enfermedad ha sido modelada como una función lineal en escala logarítmica en la incidencia con el fin de entender mejor las tendencias de crecimiento.

$info: Contiene varios componentes importantes del análisis:

$r (daily growth rate) Tasa de crecimiento diaria: 0.04145251

La tasa de crecimiento diaria estimada del brote es de 0.0415. Esto significa que cada día la cantidad de casos está creciendo en un 4.15% con respecto al día anterior, bajo la suposición de un crecimiento exponencial constante durante el periodo modelado.

Si quisiera acceder a esta información sin ingresar al modelo podría hacerlo con el siguiente código:

R

tasa_crecimiento_diaria <- ajuste_modelo$info$r
cat("La tasa de crecimiento diaria es:", tasa_crecimiento_diaria, "\n")

OUTPUT

La tasa de crecimiento diaria es: 0.04145251

$r.conf (confidence interval): 2.5 % 0.02582225 97.5 % 0.05708276

El intervalo de confianza del 95% para la tasa de crecimiento diaria está entre 0.0258 (2.58%) y 0.0571 (5.71%).

$doubling (doubling time in days): 16.72148

El tiempo de duplicación estimado del número de casos nuevos es de aproximadamente 16.72 días. Esto significa que, bajo el modelo actual y con la tasa de crecimiento estimada, se espera que el número de casos de la curva epidémica actual se duplique cada 16.72 días.

$doubling.conf (confidence interval): 2.5 % 12.14285 97.5 % 26.84302

El intervalo de confianza del 95% para el tiempo de duplicación está entre aproximadamente 12.14 y 26.84 días. Este amplio rango refleja la incertidumbre en la estimación y puede ser consecuencia de la variabilidad en los datos o de un tamaño de muestra pequeño.

$pred: Contiene las predicciones de incidencia observada. Incluye las fechas, la escala de tiempo en días desde el inicio del brote, los valores ajustados (predicciones) y los límites inferior y superior del intervalo de confianza para las predicciones.

Si quiere conocer un poco más de este componente puede explorarlo con la función glimpse.

R

glimpse(ajuste_modelo$info$pred)

¿El modelo se ajusta bien a los datos? Verifique el $R^2$

R

AjusteR2modelo <- summary(ajuste_modelo$model)$adj.r.squared
cat("El R cuadrado ajustado es:", AjusteR2modelo, "\n")

OUTPUT

El R cuadrado ajustado es: 0.7551113

Antes de continuar ¿Considera más adecuado usar una gráfica semanal para buscar un ajuste de los datos? ¿Por qué?

¿Es preferible calcular la tasa de crecimiento diaria con el ajuste semanal y no con el ajuste diario?

Grafique la incidencia incluyendo una línea que represente el modelo.

Con plot

R

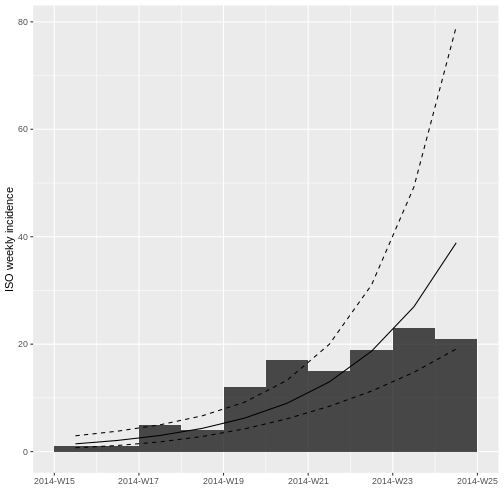
plot(incidencia_semanal, fit = ajuste_modelo)

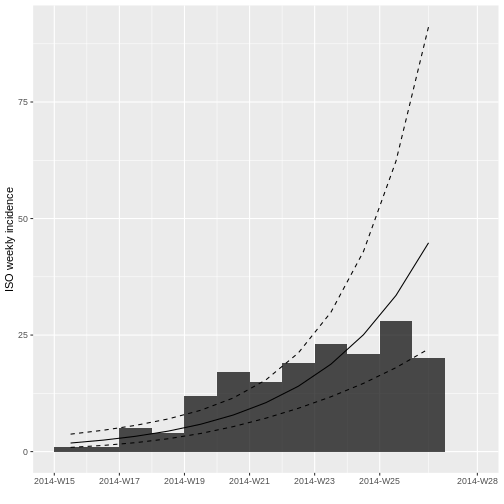
Tras ajustar el modelo log-lineal a la incidencia semanal para estimar la tasa de crecimiento de la epidemia, el gráfico muestra la curva de ajuste superpuesta a la incidencia semanal observada.

Al final del gráfico se puede observar que la incidencia semanal disminuye.

¿Porqué cree que podría estar pasando esto? ¿Cómo lo solucionaría?

4.2. Modelo log-lineal con datos truncados

Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los rezagos (biológicos y administrativos).

Dado que esta epidemia es de Ébola y la mayoría de los casos van a ser hospitalizados, es muy probable que la mayoría de las notificaciones ocurran en el momento de la hospitalización. De tal manera que podríamos examinar cuánto tiempo transcurre entre la fecha de inicio de síntomas y la fecha de hospitalización para hacernos una idea del rezago para esta epidemia.

R

summary(as.numeric(casos$fecha_de_hospitalizacion - casos$fecha_inicio_sintomas))

OUTPUT

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    1.00    2.00    3.53    5.00   22.00

Al restar la fecha de hospitalización a la fecha de inicio de síntomas podría haber valores negativos. ¿Cuál cree que sea su significado? ¿Ocurre en este caso?

Para evitar el sesgo debido a rezagos en la notificación, se pueden truncar los datos de incidencia. Pruebe descartar las últimas dos semanas. Este procedimiento permite concentrarse en el periodo en que los datos son más completos para un análisis más fiable.

Semanas a descartar al final de la epicurva

R

semanas_a_descartar <- 2
fecha_minima <- min(incidencia_diaria$dates)
fecha_maxima <- max(incidencia_diaria$dates) - semanas_a_descartar * 7

# Para truncar la incidencia semanal
incidencia_semanal_truncada <- subset(incidencia_semanal, 
                         from = fecha_minima, 
                         to = fecha_maxima) # descarte las últimas semanas de datos

# Incidencia diaria truncada. No la usamos para la regresión lineal pero se puede usar más adelante
incidencia_diaria_truncada <- subset(incidencia_diaria, 
                        from = fecha_minima, 
                        to = fecha_maxima) # eliminamos las últimas dos semanas de datos

Desafío 6

Ahora utilizando los datos truncados incidencia_semanal_truncada vuelva a ajustar el modelo logarítmico lineal.

OUTPUT

<incidence_fit object>

$model: regression of log-incidence over time

$info: list containing the following items:
  $r (daily growth rate):
[1] 0.05224047

  $r.conf (confidence interval):
          2.5 %    97.5 %
[1,] 0.03323024 0.0712507

  $doubling (doubling time in days):
[1] 13.2684

  $doubling.conf (confidence interval):
        2.5 %   97.5 %
[1,] 9.728286 20.85893

  $pred: data.frame of incidence predictions (10 rows, 5 columns)

¿Cámo interpreta estos resultados? ¿Compare los $R^2$?

Desafío 7

Ahora utilizando los datos truncados incidencia_semanal_truncada vuelva a graficar el modelo logarítmico lineal.

¿Qué cambios observa?

Observe las estadísticas resumidas del ajuste:

R

summary(ajuste_modelo_truncado$model)

OUTPUT


Call:
stats::lm(formula = log(counts) ~ dates.x, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.73474 -0.31655 -0.03211  0.41798  0.65311 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.186219   0.332752   0.560 0.591049    
dates.x     0.052240   0.008244   6.337 0.000224 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5241 on 8 degrees of freedom
Multiple R-squared:  0.8339,	Adjusted R-squared:  0.8131 
F-statistic: 40.16 on 1 and 8 DF,  p-value: 0.0002237

El modelo muestra que hay una relación significativa (R-squared: 0.8131) entre el tiempo (dates.x) y la incidencia de la enfermedad, por lo que concluimos que la enfermedad muestra un crecimiento exponencial a lo largo del tiempo.

4.3. Tasa de crecimiento y tasa de duplicación: extracción de datos

Estimacion de la tasa de crecimiento

Para estimar la tasa de crecimiento de una epidemia utilizando un modelo log-lineal es necesario realizar un ajuste de regresión a los datos de incidencia. Dado que ya tiene un objeto de incidencia truncado y un modelo log-lineal ajustado, puede proceder a calcular la tasa de crecimiento diaria y el tiempo de duplicación de la epidemia.

El modelo log-lineal proporcionará los coeficientes necesarios para estos cálculos. Note que el coeficiente asociado con el tiempo (la pendiente de la regresión) se puede interpretar como la tasa de crecimiento diaria cuando el tiempo se expresa en días.

Con el modelo ajustado truncado, es hora de realizar la estimación de la tasa de crecimiento. Estos datos los puede encontrar en el objeto ajuste modelo semana, que tiene los datos ajustados de incidencia semanal truncada.

Desafío 8

Por favor escriba el código para obtener los siguientes valores:

OUTPUT

La tasa de crecimiento diaria es: 0.05224047

OUTPUT

Intervalo de confianza de la tasa de crecimiento diaria (95%): 0.03323024 0.0712507

Si no lo recuerda, vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal

Ahora que ya ha obtenido la tasa de crecimiento diaria y sus intervalos de confianza, puede pasar a estimar el tiempo de duplicación.

Estimación del tiempo de duplicación

Esta información también la encontrará calculada y lista para utilizar en el objeto ajuste_modelo_truncado, que tiene los datos ajustados de incidencia semanal truncada.

Desafío 9

Por favor escriba el código para obtener los siguientes valores:

OUTPUT

El tiempo de duplicación de la epidemia es 13.2684 días

OUTPUT

Intervalo de confianza del tiempo de duplicación (95%): 9.728286 20.85893

Si no lo recuerda vuelva por pistas a la sección Ajuste un modelo log-lineal a los datos de incidencia semanal

5. Estimación de número de reproducción

Evaluar la velocidad a la que se propaga una infección en una población es una tarea importante a la hora de informar la respuesta de salud pública a una epidemia.

Los números de reproducción son métricas típicas para monitorear el desarrollo de epidemias y son informativos sobre su velocidad de propagación. El Número de reproducción básico $R_0$, por ejemplo, mide el número promedio de casos secundarios producidos por un individuo infeccioso dada una población completamente susceptible. Esta hipótesis suele ser válida solo al inicio de una epidemia.

Para caracterizar el la propagación en tiempo real es más común utilizar el Número de reproducción instantáneo $R_t$, el cual describe el número promedio de casos secundarios generados por un individuo infeccioso en el tiempo $t$ dado que no han habido cambios en las condiciones actuales.

En esta sección exploraremos los conceptos necesarios para calcular el Número de reproducción instantáneo, así como los pasos a seguir para estimarlo por medio del paquete de R EpiEstim.

5.1. Intervalo serial (SI)

¿Qué es el intervalo serial?

El intervalo serial en epidemiología se refiere al tiempo que transcurre entre el momento en que una persona infectada (el caso primario) comienza a mostrar síntomas y el momento en que la persona que fue infectada por ella (el caso secundario) comienza a mostrar síntomas.

Este intervalo es importante porque ayuda a entender qué tan rápido se está propagando una enfermedad y a diseñar estrategias de control como el rastreo de contactos y la cuarentena. Si el intervalo serial es corto, puede significar que la enfermedad se propaga rápidamente y que es necesario actuar con urgencia para contenerla. Si es largo, puede haber más tiempo para intervenir antes de que la enfermedad se disemine ampliamente.

Para este brote de Ébola asumiremos que el intervalo serial está descrito por una distribución Gamma de media (mean_si) de 8.7 días y con una desviación estándar (std_si) de 6.1 días. En la práctica del día 4 estudiaremos cómo estimar el intervalo serial.

R

# Parametros de la distribución gamma para el invertavlo serial
mean_si <- 8.7
std_si <-  6.1

config <- make_config(list(mean_si = mean_si, std_si = std_si)) 
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.

5.2. Estimación de la transmisibilidad variable en el tiempo, R(t)

Cuando la suposición de que ($R$) es constante en el tiempo se vuelve insostenible, una alternativa es estimar la transmisibilidad variable en el tiempo utilizando el Número de reproducción instantáneo ($R_t$). Este enfoque, introducido por Cori et al. (2013), se implementa en el paquete EpiEstim, el cual estima el $R_t$ para ventanas de tiempo personalizadas, utilizando una distribución de Poisson. A continuación, estimamos la transmisibilidad para ventanas de tiempo deslizantes de 1 semana (el valor predeterminado de estimate_R):

R

config <- make_config(list(mean_si = mean_si, std_si = std_si)) 
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.

R

# use estimate_R using method = "parametric_si"
estimacion_rt <- estimate_R(incidencia_diaria_truncada, method = "parametric_si", 
                            si_data = si_data,
                            config = config)
# Observamos las primeras estimaciones de R(t)
head(estimacion_rt$R[, c("t_start", "t_end", "Median(R)", 
                         "Quantile.0.025(R)", "Quantile.0.975(R)")])

OUTPUT

  t_start t_end Median(R) Quantile.0.025(R) Quantile.0.975(R)
1       2     8        NA                NA                NA
2       3     9  2.173592         0.3136801          7.215718
3       4    10  2.148673         0.3100840          7.132996
4       5    11  2.060726         0.2973920          6.841036
5       6    12  1.960940         0.2829915          6.509775
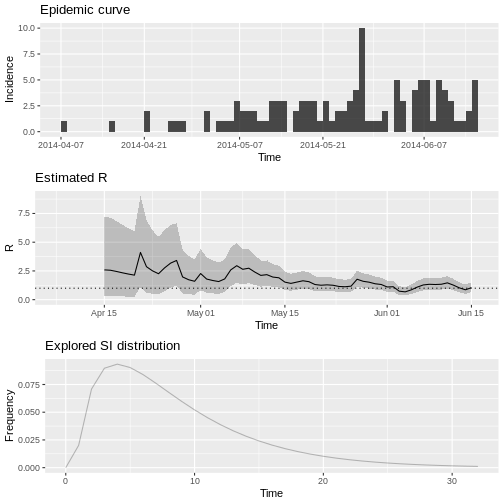
6       7    13  1.869417         0.2697834          6.205943

Grafique la estimación de $R$ como función del tiempo:

R

plot(estimacion_rt, legend = FALSE)

Sobre este documento

Este documento ha sido una adaptación de los materiales originales disponibles en RECON Learn

Contribuciones

Autores originales:

Anne Cori
Natsuko Imai
Finlay Campbell
Zhian N. Kamvar
Thibaut Jombart

Cambios menores y adaptación a español:

José M. Velasco-España
Cándida Díaz-Brochero
Nicolas Torres
Zulma M. Cucunubá

Puntos clave

Revise si al final de esta lección adquirió estas competencias:

Identificar los parámetros necesarios en casos de transmisión de enfermedades infecciosas de persona a persona.
Estimar la probabilidad de muerte (CFR).
Calcular y graficar la incidencia.
Estimar e interpretar la tasa de crecimiento y el tiempo en el que se duplica la epidemia.
Estimar e interpretar el número de reproducción instantáneo de la epidemia.

Content from Día 4 – Tutorial Serofoi

Last updated on 2024-03-12 | Edit this page

Overview

Questions

¿Cómo estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos usando serofoi?

Objectives

Al final de este taller usted podrá:

Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.

1. Introducción

serofoi es un paquete de R para estimar retrospectivamente la Fuerza de Infección de un patógeno a partir de encuestas serológicas poblacionales de prevalencia desagregadas por edad mediante la implementación de modelos Bayesianos. Para ello, serofoi utiliza el paquete Rstan, que proporciona una interfaz para el lenguaje de programación estadística Stan, mediante el cual se implementan métodos de Monte-Carlo basados en cadenas de Markov.

Como un caso particular, estudiaremos un brote de Chikungunya, una enfermedad viral descubierta en Tanzania en el año 1952 que se caracteriza por causar fuertes fiebres, dolor articular, jaqueca, sarpullidos, entre otros síntomas. Desde el año 2013, casos de esta enfermedad comenzaron a ser reportados en América y desde entonces la enfermedad ha sido endémica en varios países latinoamericanos. Durante este tutorial, vamos a analizar una encuesta serológica realizada entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue realizada poco tiempo después de una epidemia de esta enfermedad, con el fin de caracterizar los patrones endémicos o epidémicos en la zona.

2. Objetivos

Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.

3. Conceptos básicos a desarrollar

En esta práctica se desarrollarán los siguientes conceptos:

Encuestas serologícas (sero)
Fuerza de infección (foi)
Modelos serocatalíticos
Estadística Bayesiana
Visualización e interpretación de resultados de modelos FoI

La Fuerza de Infección (FoI, por sus siglas en inglés), también conocida cómo la tasa de riesgo o la presión de infección, representa la tasa a la que los individuos susceptibles se infectan dado que estuvieron expuestos a un patógeno. En otras palabras, la FoI cuantifica el riesgo de que un individuo susceptible se infecte en un periodo de tiempo.

Como veremos a continuación, este concepto es clave en el modelamiento de enfermedades infecciosas. Para ilustrar el concepto, consideremos una población expuesta a un patógeno y llamemos $P(t)$ a la proporción de individuos que han sido infectados al tiempo $t$. Suponiendo que no hay sero-reversión, la cantidad $1 - P(t)$ representa la cantidad de individuos susceptibles a la enfermedad, de tal forma que la velocidad de infección está dada por:

\[ \tag{1} \frac{dP(t)}{d t} = \lambda(t) (1- P(t)),\]

en donde $\lambda(t)$ representa la tasa a la que los individuos susceptibles se infectan por unidad de tiempo (días, meses, años, …), es decir la FoI. La ecuación diferencial (1) se asemeja a la de una reacción química en donde $P(t)$ representa la proporción de sustrato que no ha entrado en contacto con un reactivo catalítico, por lo que este tipo de modelos se conocen como modelos serocatalíticos (Muench, 1959).

A pesar de la simpleza del modelo representado por la ecuación (1), en comparación con modelos compartimentales (por ejemplo), la dificultad para conocer una condición inicial para la seropositividad en algún punto del pasado imposibilita su uso práctico. Para sortear esta limitación, es común aplicar el modelo para cohortes de edad en lugar de para el total de la población. Para ello, etiquetemos cada cohorte de edad de acuerdo con su año de nacimiento $\tau$, y supongamos que los individuos son seronegativos al nacer: \[ \frac{dP^\tau (t)}{dt} = \lambda(t) (1 - P^\tau(t)). \] Con condiciones iniciales dadas por $P^\tau(\tau) = 0$. Esta ecuación se puede resolver analíticamente, dando como resultado (Hens et al, 2010):

\[ P^{\tau} (t) = 1 - \exp\left(-\int_{\tau}^{t} \lambda (t') dt' \right). \]

Suponiendo que la FoI se mantiene constante a lo largo de cada año, la versión discreta de esta ecuación es:

\[ \tag{2} P^\tau(t) = 1 - \exp\left(-\sum_{i = \tau}^{t} \lambda_i \right), \] Como un ejemplo, consideremos la FoI representada en la siguiente figura:

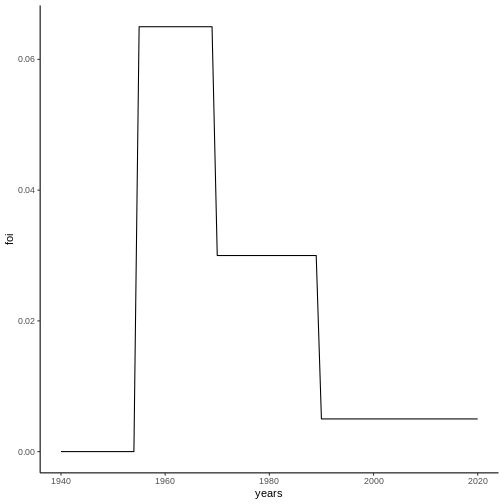
A partir de esta FoI, es posible calcular la seroprevalencia para distintas cohortes por medio de la ecuación (2):

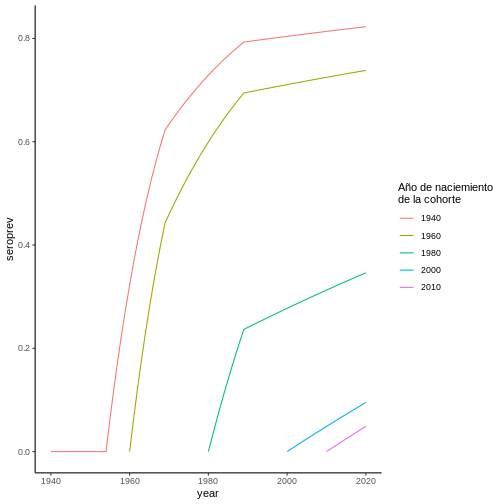
Cuando conocemos los datos de una encuesta serológica, la información a la que tenemos acceso es a una fotografía de la seroprevalencia en el momento su realización $t_{sur}$ como función de la edad de los individuos en ese momento, la cual coincide con la ecuación (2) ya que los individuos envejecen al mismo ritmo al que pasa el tiempo; es decir:

\[ \tag{3} P^{t_{sur}}(a^\tau) = 1 - \exp\left(-\sum_{i = \tau}^{t_{sur}} \lambda_i \right). \] En el caso del ejemplo, esto nos da la siguiente gráfica: 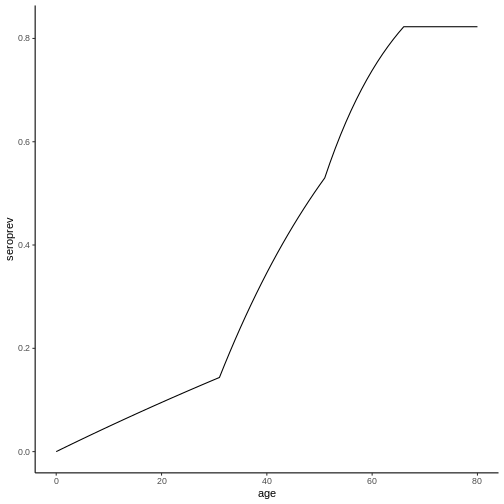Note que los valores de seroprevalencia de cada edad en esta gráfica corresponden a los valores de seroprevalencia al momento de la encuesta (2020) en la gráfica anterior.

La misión que cumple serofoi es estimar la fuerza de infección histórica $\lambda(t)$ a partir de esta fotografía del perfil serológico de la población al momento de la encuesta. para lo cual se requieren encuestas serológicas que cumplan con los siguientes criterios de inclusión:

Basadas en poblacionales (no hospitalaria).
Estudio de tipo transversal (un solo tiempo) .
Que indique la prueba diagnóstica utilizada.
Que identifique la edad del paciente en el momento de la encuesta.

En casos donde la FoI pueda considerarse constante, la ecuación (3) da como resultado:

\[ \tag{4} P_{sur}(a^\tau(t_{sur})) = 1 - \exp (-\lambda a^\tau), \]

en donde se tuvo en cuenta qué, al momento de la introducción del patógeno ($t = 0$), la proporción de individuos infectados fue $P(0) = 0$ (condición inicial). Note que el término de la suma en la ecuación (3) da como resultado la edad de cada cohorte al considerar la fuerza de infección constante.

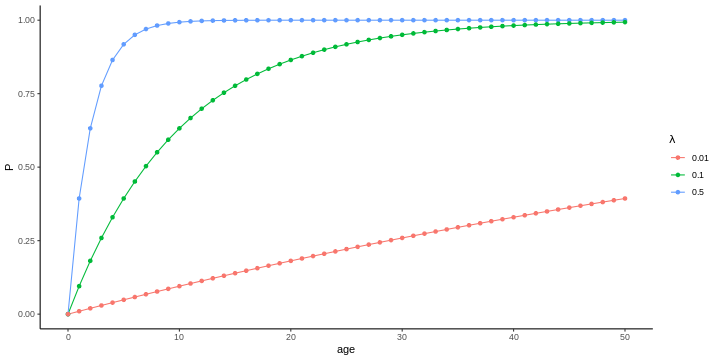
Figura 1. Curvas de prevalencia en función de la edad para distintos valores de FoI constante.

En este ejemplo hemos escogido, por simplicidad, que la FoI fuese constante; sin embargo, este no es necesariamente el caso. Identificar si la FoI sigue una tendencia constante o variante en el tiempo puede ser de vital importancia para la identificación y caracterización de la propagación de una enfermedad. Es acá donde el paquete de R serofoi juega un papel importante, ya que este permite estimar retrospectivamente la FoI de un patógeno, recuperando así su evolución temporal, por medio de modelos Bayesianos pre-establecidos.

Los modelos actuales del paquete serofoi asumen los siguientes supuestos biológicos:

No hay sero-reversión (sin pérdida de inmunidad).
La FoI no depende de la edad.
Bajos o nulos niveles de migración en las poblaciones.
Diferencias pequeñas entre las tasas de mortalidad de susceptibles e infectados.

3.2. Modelos Bayesianos

A diferencia del enfoque frecuentista, donde la probabilidad se asocia con la frecuencia relativa de la ocurrencia de los eventos, la estadística Bayesiana se basa en el uso de la probabilidad condicional de los eventos respecto al conocimiento (o estado de información) que podamos tener sobre los datos o sobre los parámetros que queramos estimar.

Por lo general, cuando proponemos un modelo lo que buscamos es disminuir la incertidumbre sobre algún parámetro, de tal forma que nos aproximemos a su valor tan óptimamente como nos lo permita nuestro conocimiento previo del fenómeno y de las mediciones realizadas (datos).

La inferencia Bayesiana se sustenta en el teorema de Bayes, el cual establece que: dado un conjunto de datos $\vec{y} = (y_1, …, y_N)$, el cual representa un único evento, y la variable aleatoria $\theta$, que representa un parámetro de interés para nosotros (en nuestro caso, la FoI $\lambda$), la distribución de probabilidad conjunta de las variables aleatorias asociadas está dada por:

\[ \tag{4} p(\vec{y}, \theta) = p(\vec{y} | \theta) p(\theta) = p(\theta | \vec{y}) p(\vec{y}), \]

de donde se desprende la distribución aposteriori de $\theta$, es decir una versión actualizada de la distribución de probabilidad de la FoI condicionada a nuestros datos:

\[\tag{5} p(\theta, \vec{y}) = \frac{p(\vec{y} | \theta) p(\theta)}{p(\vec{y})},\]

La distribución $p(\vec{y} | \theta)$, que corresponde a la información interna a los datos condicionada al valor del parámetro $\theta$, suele estar determinada por la naturaleza del experimento: no es lo mismo escoger pelotas dentro de una caja reemplazándolas que dejándolas por fuera de la caja (e.g.). En el caso particular de la FoI, contamos con datos como el número total de encuestas por edad y el número de casos positivos, por lo que es razonable asignar una distribución binomial a la probabilidad, como veremos a continuación.

3.3.1. Modelo FoI constante

En nuestro caso particular, el parámetro que queremos estimar es la FoI ($\lambda$). La distribución de probabilidad apriori de $\lambda$ representa nuestras suposiciones informadas o el conocimiento previo que tengamos sobre el comportamiento de la FoI. En este contexto, el estado de mínima información sobre $\lambda$ está representado por una distribución uniforme:

\[\tag{6} \lambda \sim U(0, 2),\]

lo que significa que partimos de la premisa de que todos los valores de la fuerza de infección entre $0$ y $2$ son igualmente probables. Por otro lado, de la teoría de modelos sero-catalíticos sabemos que la seroprevalencia en un año dado está descrita por un proceso cumulativo con la edad (Hens et al, 2010):

\[\tag{7} P(a, t) = 1 - \exp\left( -\sum_{i=t-a+1}^{t} \lambda_i \right), \] en donde $\lambda_i$ corresponde a la FoI al tiempo $t$. Como en este caso la FoI es constante, la ec. (7) se reduce a:

\[\tag{8} P(a, t) = 1 - \exp\left( -\lambda a \right),\]

Si $n(a, t_{sur})$ es el número de muestras positivas por edad obtenidas en un estudio serológico desarrollado en el año $t_{sur}$, entonces podemos estimar la distribución de los casos seropositivos por edad condicionada al valor de $\lambda$ como una distribución binomial:

\[\tag{9} p(a, t) \sim Binom(n(a, t), P(a, t)) \\ \lambda \sim U(0, 2)\]

3.3.2. Modelo FOI dependientes del tiempo

Actualmente, serofoi permite la implementación de dos modelos dependientes del tiempo: uno de variación lenta de la FoI (tv-normal) y otro de variación rápida (tv-normal-log) de la FoI.

Cada uno de ellos se basa en distintas distribuciones previas para $\lambda$, las cuales se muestran en la tabla 1.

Model Option	Probability of positive case at age $a$	Prior distribution
`constant`	$\sim binom(n(a,t), P(a,t))$	$\lambda\sim uniform(0,2)$
`tv_normal`	$\sim binom(n(a,t), P(a,t))$	$\lambda\sim normal(\lambda(t-1),\sigma)\\ \lambda(t=1)\sim normal(0,1)$
`tv_normal_log`	$\sim binom(n(a,t), P(a,t))$	$\lambda\sim normal(log(\lambda(t-1)),\sigma)\\ \lambda(t=1)\sim normal(-6,4)$

Tabla 1. Distribuciones a priori de los distintos modelos soportados por serofoi. $\sigma$ representa la desviación estándar.

Como se puede observar, las distribuciones previas de $\lambda$ en ambos casos están dadas por distribuciones Gaussianas con desviación estándar $\sigma$ y centradas en $\lambda$ (modelo de variación lenta - tv_normal) y $\log(\lambda)$ (modelo de variación rápida - tv_normal_log). De esta manera, la FoI en un tiempo $t$ está distribuida de acuerdo a una distribución normal alrededor del valor que esta tenía en el tiempo inmediatamente anterior. El logaritmo en el modelo tv_normal_log permite identificar cambios drásticos en la tendencia temporal de la FoI.

4. Contenido del taller

4.1 Instalación de serofoi

Previo a la instalación de serofoi, cree un proyecto en R en la carpeta de su escogencia en su máquina local; esto con el fin de organizar el espacio de trabajo en donde se guardarán los códigos que desarrolle durante la sesión.

Antes de realizar la instalación de serofoi, es necesario instalar y configurar C++ Toolchain (instrucciones para windows/ mac/linux). Después de haber configurado C++ Toolchain, ejecute las siguientes líneas de código para instalar el paquete:

R

if(!require("pak")) install.packages("pak")
pak::pak("epiverse-trace/serofoi")

Opcionalmente, es posible modificar la configuración de R para que los modelos a implementar corran en paralelo, aprovechando los núcleos del procesador de su computador. Esto tiene el efecto de disminuir los tiempos de cómputo de las implementaciones en Stan. Para activar esta opción ejecute:

R

options(mc.cores=parallel::detectCores())

Finalmente, cargue el paquete ejecutando:

R

library(serofoi)

4.2 Caso de uso: Chikungunya

En esta sección vamos a analizar una encuesta serológica realizada entre octubre y diciembre de 2015 en Bahía, Brasil, la cual fue realizada poco tiempo después de una epidemia de esta enfermedad en la zona. Nuestro objetivo es caracterizar la propagación de la enfermedad por medio de la implementación de los distintos modelos y determinar cuál de estos describe mejor la situación. Primero, carguemos y preparemos los datos que utilizaremos en este análisis. La base chik2015 contiene los datos correspondientes a esta encuesta serológica:

R

data(chik2015)
chik2015p <- prepare_serodata(chik2015)
str(chik2015p)

OUTPUT

'data.frame':	4 obs. of  16 variables:
 $ survey        : chr  "BRA 2015(S019)" "BRA 2015(S019)" "BRA 2015(S019)" "BRA 2015(S019)"
 $ total         : int  45 109 144 148
 $ counts        : num  17 55 63 69
 $ age_min       : num  1 20 40 60
 $ age_max       : num  19 39 59 79
 $ tsur          : num  2015 2015 2015 2015
 $ country       : Factor w/ 256 levels "ABW","AFG","AGO",..: 33 33 33 33
 $ test          : chr  "ELISA" "ELISA" "ELISA" "ELISA"
 $ antibody      : chr  "IgG anti-CHIKV" "IgG anti-CHIKV" "IgG anti-CHIKV" "IgG anti-CHIKV"
 $ reference     : chr  "Dias et al. 2018" "Dias et al. 2018" "Dias et al. 2018" "Dias et al. 2018"
 $ age_mean_f    : num  10 29 49 69
 $ sample_size   : int  446 446 446 446
 $ birth_year    : num  2005 1986 1966 1946
 $ prev_obs      : num  0.378 0.505 0.438 0.466
 $ prev_obs_lower: num  0.238 0.407 0.355 0.384
 $ prev_obs_upper: num  0.535 0.602 0.523 0.55

Para correr el modelo de FoI constante y visualizar los resultados del mismo, corra las siguientes líneas de código:

R

chik_constant <- run_seromodel(serodata = chik2015p,
                               foi_model = "constant",
                               n_iters = 1000)

chik_constant_plot <- plot_seromodel(chik_constant, 
                                     serodata = chik2015p, 
                                     size_text = 12)

Ahora, corra los modelos dependientes del tiempo con n_iters =1500. Luego visualice conjuntamente las tres gráficas por medio de la función plot_grid() del paquete cowplot:

R

cowplot::plot_grid(chik_constant_plot, 
                   chik_normal_plot, 
                   chik_normal_log_plot,
                   ncol = 3)

NOTA: Debido a que el número de trayectorias es relativamente alto, con el fin de asegurar la convergencia de los modelos, el tiempo de cómputo de los modelos dependientes del tiempo puede tardar varios minutos.

Pista: Debería obtener la siguiente gráfica:

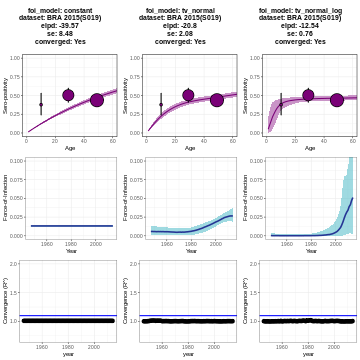
Explicación de elpd (expected log pointwise predictive density)

5. Reflexión

Según los criterios explicados anteriormente, responda:

¿Cuál de los tres modelos se ajusta mejor a esta encuesta serológica?

¿Cómo interpreta estos resultados?

Reto

Una vez terminado el tutorial proceda a realizar el Reto.

Puntos Clave

Revise si al final de esta lección adquirió estas competencias:

Explorar y analizar una encuesta serológica típica.
Aprender a estimar la Fuerza de Infección en un caso de uso específico.
Visualizar e interpretar los resultados.

Sobre este documento

Este documento ha sido diseñado por Nicolás Torres Domínguez para el Curso Internacional: Análisis de Brotes y Modelamiento en Salud Pública, Bogotá 2023. TRACE-LAC/Javeriana.

Contribuciones

Nicolás Torres Domínguez
Zulma M. Cucunuba

Contribuciones son bienvenidas vía pull requests.

Referencias

Muench, H. (1959). Catalytic models in epidemiology. Harvard University Press.

Hens, N., Aerts, M., Faes, C., Shkedy, Z., Lejeune, O., Van Damme, P., & Beutels, P. (2010). Seventy-five years of estimating the force of infection from current status data. Epidemiology & Infection, 138(6), 802–812.

Cucunubá, Z. M., Nouvellet, P., Conteh, L., Vera, M. J., Angulo, V. M., Dib, J. C., … Basáñez, M. G. (2017). Modelling historical changes in the force-of-infection of Chagas disease to inform control and elimination programmes: application in Colombia. BMJ Global Health, 2(3). doi:10.1136/bmjgh-2017-000345

Content from Día 5 – Tutorial Vaccineff: Introducción al cálculo de efectividad vacunal con cohortes usando vaccineff

Last updated on 2024-03-12 | Edit this page

Overview

Questions

¿Cómo realizar el cálculo de efectividad vacunal con cohortes usando vaccineff?

Objectives

Al final de este taller usted podrá:

Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes

1. Introducción

En esta sesión se espera que los participantes se familiaricen con uso del paquete de Rvaccineff. Utilizaremos el diseño de cohortes para estimar la efectividad vacunal de un conjunto de datos de prueba y analizaremos los resultados obtenidos.

2. Objetivos

Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes

3. Conceptos básicos a desarrollar

En esta práctica se desarrollarán los siguientes conceptos:

Eficacia y Efectividad vacunal
Tiempo de inducción o “delays” en el análisis de efectividad de vacunas
Diseños observacionales para el estudio de la efectividad vacunal
Diseño de cohortes para estimación de la efectividad vacunal
Estimador no paramétrico Kaplan-Meier
Modelo semi-paramétrico de Cox
Riesgos proporcionales

3.1. Eficacia vs Efectividad vacunal

Eficacia:

Se refiere a la capacidad de lograr un efecto deseado o esperado bajo condiciones ideales o controladas.
Es una medida teórica. En experimentos clínicos, por ejemplo, la eficacia de un medicamento se evalúa en condiciones controladas, donde todos los factores externos están cuidadosamente regulados para determinar el rendimiento puro del medicamento.
Puede considerarse como “lo que puede hacer” una intervención en las mejores circunstancias posibles.

Efectividad:

Se refiere a qué tan bien funciona una intervención en condiciones “reales” o prácticas, fuera de un entorno controlado.
Es una medida práctica. En el contexto de los medicamentos, la efectividad se refiere a qué tan bien funciona un medicamento en el “mundo real”, donde las condiciones no están tan controladas y hay muchos factores variables.
Puede considerarse como “lo que realmente hace” una intervención en circunstancias típicas o cotidianas.

Un ejemplo podría ser un medicamento que en experimentos clínicos (en condiciones ideales) mostró una eficacia del 95% en prevenir el desenlace. Sin embargo, cuando se usó en el contexto general, considerando factores como la adherencia al tratamiento, interacciones con otros medicamentos y variabilidad en la población, su efectividad fue del 85%. Aquí, la eficacia muestra el potencial del medicamento bajo condiciones ideales, mientras que la efectividad muestra cómo funciona en situaciones cotidianas.

En el caso de las vacunas la efectividad hace referencia a la disminución proporcional de casos de una enfermedad o evento en una población vacunada comparada con una población no vacunada, en condiciones del mundo real.

3.2. Tiempo de inducción

El tiempo de inducción o “delay” se refiere al periodo necesario para que la vacuna administrada induzca una respuesta inmune protectora frente a la infección o la enfermedad provocada por un patógeno. Si ocurre una infección entre el momento de la vacunación y el momento donde se prevé exista una respuesta inmune protectora, ocurrirá la infección de manera natural y no se considera un fallo de la vacuna en cuestión, puesto que la persona inmunizada aún no contaba con la protección conferida por la vacuna.

3.3. Diseños observacionales para el estudio de la efectividad vacunal

Por múltiples razones, los estudios observacionales son los más utilizados en la estimación de la efectividad vacunal. Existen múltiples diseños, entre ellos: diseño de cohortes, diseño de casos y controles, diseño de test-negativo, diseño “screening-method”. La elección del diseño, dependerá de la disponibilidad de información y los recursos disponibles para llevar a cabo el estudio.

3.4. Diseño de cohorte para el estudio de la efectividad vacunal

El término cohorte se refiere a un grupo de personas que comparten una característica común. En los estudios con diseño de cohorte, existen dos o más poblaciones que difieren en una característica o exposición y se realiza un seguimiento a ambos grupos para evaluar la aparición de uno o más desenlaces de interés y comparar la incidencia de los eventos entre ambos grupos. Para el caso de los estudios de la efectividad de vacunas, la exposición de interés corresponde a la aplicación de la vacuna y los desenlaces pueden incluir:

Infección: contagio con el patógeno de interés tras una exposición a alguien infeccioso
Enfermedad: desarrollo de signos y síntomas relacionados con la infección con un patógeno. Puede tener diferentes grados de severidad, requerir ingreso a hospitalización, UCI o incluso conducir a la muerte.
A la hora de llevar a cabo estos estudios se debe garantizar que las personas incluidas en cada población no tengan el desenlace de interés que será evaluado durante el seguimiento. Así mismo, es importante que el seguimiento se lleve a cabo de manera igual de rigurosa y por el mismo tiempo en ambos grupos.

La efectividad vacunal corresponde a la reducción relativa del riesgo de desarrollar la infección y/o enfermedad. En los estudios de cohorte se puede estimar el riesgo relativo, los odds ratio o los hazard ratio que expresa el riesgo que tiene la cohorte no expuesta comparado con la cohorte de los expuestos. La efectividad vacunal será, por lo tanto, el complemento del riesgo proporcional en la cohorte de expuestos.

Veamos esto con un ejemplo: para evaluar la efectividad de una vacuna para prevenir el desarrollo de enfermedad en una población, al cabo del seguimiento la incidencia en la cohorte vacunada fue de 1 por 1000 habitantes y en la cohorte no vacunada fue de 5 por 1000 habitantes. En este caso, tenemos que el riesgo relativo en la población vacunada fue 0.001/0.005 = 0,2. Es decir, la población vacunada tuvo una incidencia correspondiente al 20% de la incidencia de la población no vacunada. Esta reducción se puede atribuir a la vacuna y para estimarla usaríamos el complemento, que corresponde a 1 - 0,2= 0,8. Es decir que la reducción que se observó corresponde a un 80% y se puede atribuir a la vacuna, por lo tanto, la efectividad de la vacunación fue del 80% para evitar la enfermedad.

3.5. Métodos estadísticos para análisis de efectividad vacunal

En el diseño de cohortes se utilizan principalmente dos métodos: Estimación no paramétrica de Kapplan-Meier y Modelo semi-paramétrico de Cox

Estimador Kaplan-Meier

El estimador Kaplan-Meier utiliza las tasas de incidencia de un evento para cuantificar la probabilidad de supervivencia $S(t)$ de forma no paramétrica, es decir, sin una representación matemática funcional. En general, la incidencia acumulada de cada grupo permite cuantificar el riesgo de presentar el evento como $1 - S(t)$. Asimismo, la comparación entre el riesgo de ambos grupos en un punto del tiempo determina el riesgo relativo entre grupos ($RR$). A partir de esta se estima la efectividad vacunal como: \[V_{EFF} = 1 - RR\]

Modelo de Regresión de Cox

El modelo Cox, permite estimar de forma semi-paramétrica la función de riesgo instantáneo $\lambda(t|x_i)$ de un individuo $i$ en terminos de sus características, las cuales se asocian a un conjunto de covariables $x_1, x_2, ..., x_n$, con lo cual se tiene:

\[\lambda(t|x_i) = \lambda_0(t) \exp(\beta_1 x_{i1} + \beta_2 x_{i2} + ....+\beta_n x_{in})\] donde $\beta_1, \beta_2, ..., \beta_n$ son los coeficientes de la regresión y $\lambda_0$ es una función basal no especificada, por lo que el modelo se asume como semi-paramétrico. En el caso en el que la función de riesgo instantáneo es completamente especificada, es decir, se conoce la forma funcional de $\lambda_0(t)$, es posible calcular matemáticamente la probabilidad de supervivencia. Sin embargo, ninguna de estas funciones puede ser estimada directamente del modelo de Cox. Por el contrario, con este se busca estimar el hazard ratio, una medida de riesgos comparativa entre dos individuos $i$ y $j$ con características $x_{i1}, x_{i2}, ..., x_{in}$ y $x_{j1}, x_{j2}, ..., x_{jn}$, respectivamente. En este orden, al evaluar el riesgo de un individuo con respecto al otro se tiene:

\[HR = \frac{\lambda(t|x_i)}{\lambda(t|x_j)} = \frac{\lambda_0(t)\exp(\beta x_{i})}{\lambda_0(t)\exp(\beta x_{j})} = \exp(\beta(x_i-x_j))\] Riesgos proporcionales: Nótese que la dependencia temporal de las funciones de riesgo instantáneo individuales se canceló dentro de la expresion anterior para el Hazard ratio, por tanto se dice que los individuos $i$ y $j$ exhiben riesgos proporcionales en el tiempo. Esta hipótesis constituye un pilar importante de los estudios de efectividad bajo diseño de cohorte.

En el contexto de los estudios de cohorte, el modelo de Cox puede utilizarse para estimar el riesgo comparativo entre ambos grupos de presentar un desenlace de interés. En este sentido la pertenecia a un grupo se utiliza como covariable dentro de la regresión. Particularmente, para el cálculo de la efectividad vacunal se puede utilizar el $HR$ de forma análoga al caso discutido para el estimador Kaplan-Meier, con lo que se define:

\[V_{EFF} = 1 - HR\]

4. Caso de uso del paquete

Para esta sesión se trabajará con el conjunto de datos de ejemplo incluido en el paquete vaccineff. Adicionalmente, se utilizarán algunas funciones de los paquetes ggplot2 y cowplot para vizualizar algunos resultados.

Para installar vaccineff ejecute las siguientes líneas en R:

R

# if(!require("pak")) install.packages("pak")
# pak::pak("epiverse-trace/vaccineff@dev")

Posteriormente, para cargar los paquetes en el espacio de trabajo y el set de datos de ejemplo del vaccineff ejecute:

R

library("vaccineff")
library("ggplot2")
library("cowplot")
data(cohortdata)
head(cohortdata)

OUTPUT

  sex age subsidy death_date vaccine_date_1 vaccine_date_2 vaccine_1 vaccine_2
1   F   6       0       <NA>           <NA>           <NA>      <NA>      <NA>
2   M  79       0       <NA>     2044-03-31     2044-05-07    BRAND2    BRAND2
3   F  34       0       <NA>     2044-07-26     2044-09-03    BRAND2    BRAND2
4   M  26       0       <NA>           <NA>           <NA>      <NA>      <NA>
5   F  66       0       <NA>     2044-05-20     2044-06-17    BRAND2    BRAND2
6   M  10       1       <NA>           <NA>           <NA>      <NA>      <NA>

Este tabla contiene información de una epidemia simulada ocurrida en 2044 sobre una población hipotética, compuesta por 100.000 habitantes, que recibió dos dosis de una vacuna para disminuir el riesgo de muerte por una enfermedad respiratoria viral. Sobre esta población se realizó seguimiento por 1 año, entre el 1 de enero y 31 de diciembre de 2044. En el conjunto de datos se presenta la información desagregada para cada uno de los participantes.

4.1 Funciones básicas de exploración de datos

4.1.2 Grupo etario

Para agrupar la población por grupo etario y graficar la distribución por edad utilizaremos la función “get_age_group”. Para esto, ejectute el siguiente comando en R:

R

cohortdata$age_group <- get_age_group(
  data = cohortdata,
  col_age = "age",
  max_val = 80,
  min_val = 0,
  step = 9)

Esta función permite agrupar la población en intervalos etarios a partir de la variable “age” del conjunto de datos. En particular, para construir la agrupación por decenios se asigna el ancho del intervalo con step = 9, el mínimo valor de edad en 0 con “min_val” y el máximo valor en 80 con “max_val”. Esto significa que cualquier registro con edad mayor o igual a 80 años se agrupará en “>80”

Puede graficar de forma rápida la distribución etaria asociada a la variable “age_group” utilizando la función “geom_bar” de la librería ggplot2. Para esto, ejecute el siguiente comando en R:

R

ggplot(data = cohortdata,
  aes(x = age_group)) +
  geom_bar() +
  theme_classic()

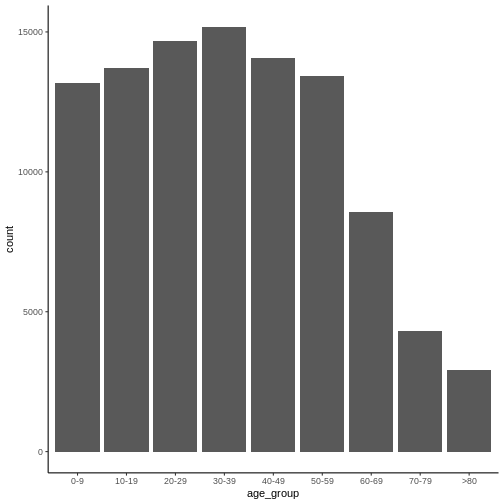
4.1.2. Cobertura vacunal en las cohortes

En un conjunto de datos típico de un estudio de cohorte se tiene información desagregada por persona de la(s) dosis aplicada(s) durante el seguimiento. En este sentido, es importante dimensionar el nivel de cobertura en la vacunación alcanzado durante el seguimiento. vaccineff ofrece la función “plot_coverage” que permite llevar a cabo esta tarea con facilidad. Para esto, ejecute el siguiente comando en R:

R

plot_coverage(
  data = cohortdata,
  vacc_date_col = "vaccine_date_1",
  unit = "month",
  doses_count_color = "steelblue",
  coverage_color = "mediumpurple",
  date_interval = NULL,
  cumulative = FALSE)

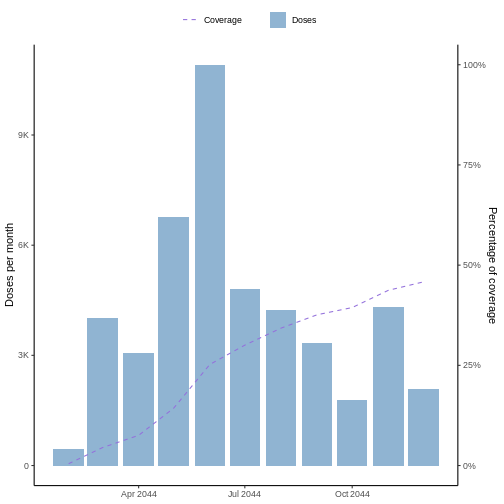
Esta función calcula la cobertura con base en alguna dosis, la cual se especifica en el parámetro “vacc_date_col”. En particular, en el ejemplo anterior se utiliza la primera dosis del conjunto de datos de ejemplo (“vaccine_date_1”). Además, es posible agrupar el conteo de dosis y el cálculo de cobertura en días, meses y años utilizando el parámetro “unit” y personalizar los colores de la gráfica con los parámetros “doses_count_color” y “coverage_color”. El parámetro “date_interval” se utiliza para personalizar el intervalo de datos que se quiere observar, en caso de usar “FALSE” la función toma las fechas mínima y máxima de la tabla. Finalmente, el parámetro “cumulative” permite graficar el conteo de dosis de forma acumulada en el tiempo.

4.2 Seguimiento de la cohorte y tiempos al evento

Para llevar a cabo la estimación de la efectividad vacunal primero debe definir la fecha de inicio y fin del seguimiento de cohortes, esto con base en su exploración de las bases de datos. Para el caso particular del conjunto de datos ejemplo contenidos es vaccineff se utiliza:

R

start_cohort <- as.Date("2044-01-01")
end_cohort <- as.Date("2044-12-31")

Para determinar la fecha de immunización, de un individuo vaccineff cuenta con la función get_immunization_date(). Esta calcula la fecha de inmunización seleccionando la vacuna que cumpla con el criterio de fecha límite presentado en la siguiente figura.

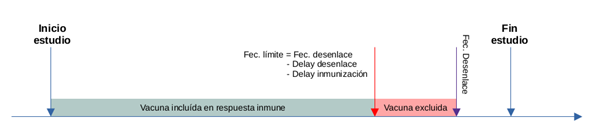
Esquema de fecha límite para selección de vacunas

4.2.2 Tiempo de inducción del efecto (delay)

En la figura anterior se introdujo el concepto de delay. El delay del desenlace hace referencia al tiempo característico al desenlace desde que se un individuo se infecta. Por otra parte, el delay de la immunización se refiere al tiempo que se espera que transcurra antes de considerar que existe inmunidad protectora. Cada uno de estas variables puede controlarse en la función mediante los parámetros outcome_delay e immunization_delay, respectivamente. El valor que se asigne a estas depende de la naturaleza del estudio. En particular, para nuestra epidemia ejemplo utilizaremos outcome_delay = 0 dado que no es considerado como una variable relevante para determinar la fecha límite en que la vacuna podría hacer efecto. Por otra parte, el valor asumido para el de immunización es de 14 días.

Para calcular la fecha de immunización de cada individiduo escriba la siguiente instrucción en R y ejecútela:

R

cohortdata$immunization <-
  get_immunization_date(
    data = cohortdata,
    outcome_date_col = "death_date",
    outcome_delay = 0,
    immunization_delay = 14,
    vacc_date_col = c("vaccine_date_1", "vaccine_date_2"),
    end_cohort = end_cohort,
    take_first = FALSE)

Al ejecutar este comando, se añadirá una columna nueva al conjunto de datos del caso de estudio, esta columna contiene una variable de tipo “Date” que corresponde la fecha 14 días posteriores a la última dosis de cualquiera de las dos vacunas utilizadas en el caso de estudio, que cumpla con el criterio de fecha límite. Puede evidenciar la nueva columna en el conjunto de datos.

4.2.3. Definir la exposición: cohorte vacunada y cohorte no vacunada

A continuación, cree una columna nueva donde categorice cada uno de los sujetos según su estado vacunal, vacunados como “v” y no vacunados como “u” (unvaccinated, en inglés). Para esto ejecute el siguiente comando en R:

R

cohortdata$vaccine_status <- set_status(
  data = cohortdata,
  col_names = "immunization",
  status = c("vacc", "unvacc"))

Al ejecutar el comando encontrará que se ha creado una nueva columna en el conjunto de datos con los valores “vacc” o “unvacc”, para cada uno de los registros de acuerdo con su estado de vacunación, el cual se determina a partir de la variable "immunization".

4.2.3 Definir el desenlace: estado vivo vs estado fallecido

El desenlace para este ejercicio va a ser la condición vital al final del estudio. En otros ejercicios el desenlace de interés podría ser la hospitalización o la infección, dependiendo del conjunto de datos utilizado.

Tenga en cuenta que en conjunto de datos del caso de estudio todas las defunciones son debidas a la infección por el virus de interés. Para definir el desenlace de interés de acuerdo a la condición vital de los participantes en la cohorte, ejecute el siguiente comando en R:

R

cohortdata$death_status <- set_status(
  data = cohortdata,
  col_names = "death_date")

Al ejecutar este comando, nuevamente aparecerá una nueva columna en el conjunto de datos con el que se está realizando el caso de estudio. Al explorar la base de datos completa, se verifica que en la nueva columna aparece 0 = vivo y 1 = fallecido.

4.2.4. Calcular el tiempo al evento (desde exposición hasta desenlace)

Ahora, calcule para cada una de las personas el tiempo que fue seguido en el estudio. Recuerde que el seguimiento se hace igual para ambas cohortes (vacunada y no vacunada) y finaliza cuando termina el estudio o cuando se presenta el desenlace de interés. Para obtener este dato ejecute el siguiente comando en R:

R

cohortdata$time_to_death <- get_time_to_event(
  data = cohortdata,
  outcome_date_col = "death_date",
  start_cohort = start_cohort,
  end_cohort = end_cohort,
  start_from_immunization = FALSE)

Nuevamente, al ejecutar este comando se creará una nueva variable en el conjunto de datos y como se puede evidenciar al explorar los datos completos, la nueva variable estima los días de seguimiento para cada una de las personas. Esta función permite crear tiempos al evento desde el inicio del seguimiento en el caso de estudio, en este caso se utiliza la opción “start_from_immunization = FALSE” o desde la fecha de inmunización. Para este último caso es necesario asignar “start_from_immunization = TRUE” y pasar el nombre de la columna con la información sobre la fecha de inmunización en el parámetro “immunization_date_col”. En la figura a continuación se presenta un esquema de los dos métodos de cálculo del tiempo al evento.

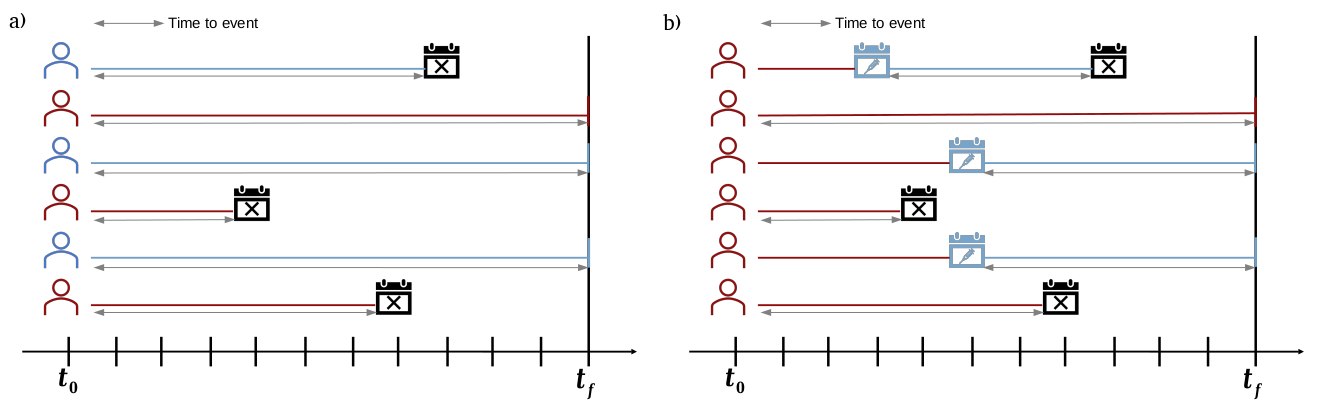
a) Tiempo al evento evaludado desde inicio de la cohorte. b) tiempo al evento desde la fecha de immunización

4.3. Curvas de riesgo acumulado y supervivencia al desenlace en cada cohorte

Como primera aproximación a la efectividad vacunal, graficaremos la curva de riesgos acumulados (1 menos la supervivencia de las poblaciones). Esta nos permite entender de forma cualitativa cuál de las poblaciones acumula mayor riesgo durante el estudio de cohorte. Y por tanto, evaluar hipótesis sobre el potencial efecto de la vacunación sobre la cohorte. Para graficar el riesgo acumulado ejecute el siguiente comando en R:

R

plot_survival(data = cohortdata,
  outcome_status_col = "death_status",
  time_to_event_col = "time_to_death",
  vacc_status_col = "vaccine_status",
  vaccinated_status = "vacc",
  unvaccinated_status = "unvacc",
  vaccinated_color = "steelblue",
  unvaccinated_color = "darkred",
  start_cohort = start_cohort,
  end_cohort = end_cohort,
  percentage = TRUE,
  cumulative = TRUE)

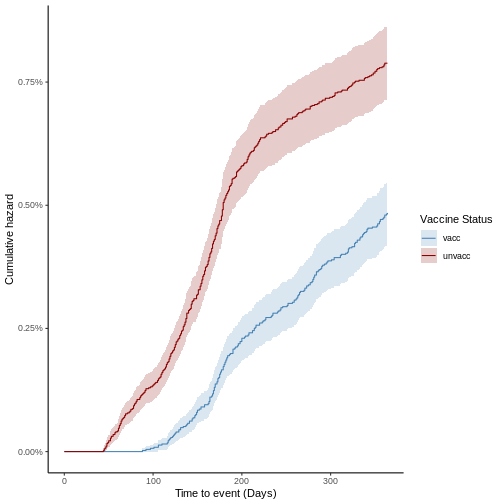
A partir de la función anterior también es posible realizar la gráfica de supervivencia de las cohortes o gráfica de Kaplan-Meier en la cual se parte del 100% de ambas cohortes en el eje de las ordenadas y en el eje de las abscisas se representa el tiempo y se observa la disminución que hay debido a las defunciones en cada cohorte. Tenga en cuenta que este no es el estimador de Kaplan-Meir, es sólo la gráfica sobre las curvas de supervivencia y de riesgo acumulado. Para obtener este gráfico, se ejecuta la misma función y se cambia el argumento “percentage” por FALSE:

R

plt_surv <- plot_survival(data = cohortdata,
  outcome_status_col = "death_status",
  time_to_event_col = "time_to_death",
  vacc_status_col = "vaccine_status",
  vaccinated_status = "vacc",
  unvaccinated_status = "unvacc",
  vaccinated_color = "steelblue",
  unvaccinated_color = "darkred",
  start_cohort = start_cohort,
  end_cohort = end_cohort,
  percentage = TRUE,
  cumulative = FALSE)
plt_surv

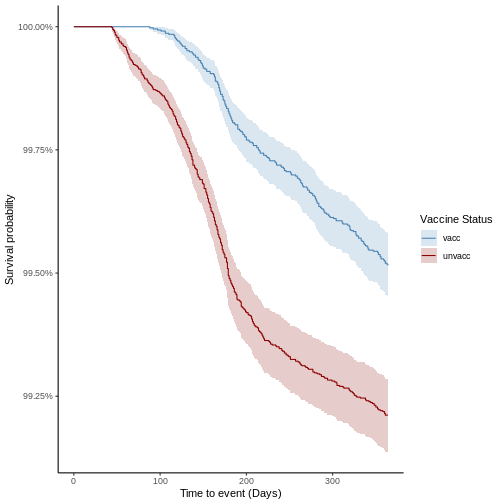
4.4. Evaluación de la hipótesis riesgos proporcionales

Previo a la estimación de la efectividad vacunal es importante testear la hipótesis de riesgos proporcionales entre las cohortes de vacunados y no vacunados, con el fin de identificar posibles sesgos muestrales que afecten la validez de los resultados y definir estrategias de cálculo de cohortes dinámicas, emparejamiento o estratificación, entre otras, que permitar contrarestar este efecto. Un método cualitativo utilizado ampliamente en la literatura es la transformación de la probabilidad de supervivencia mediante la función logaritmo natural como $\log[-\log[S(t)]]$. Al graficar esta función contra el logaritmo del tiempo al evento, es posible identificar si los grupos representan riesgos proporcionales cuando sus curvas se comportan de forma aproximadamente paralela.

A continuación se presentan las gráficas loglog obtenidas al construir los tiempos al evento de forma dinámica (panel de la izquiera) y con punto de inicio fijo (panel de la derecha). Particularmente, se observa que el cálculo dinámico de los tiempos no satisface riesgos proporcionales, por lo que pontencialmente necesitará algún tipo de estrategia para contrarestar los posibles sesgos muestrales.

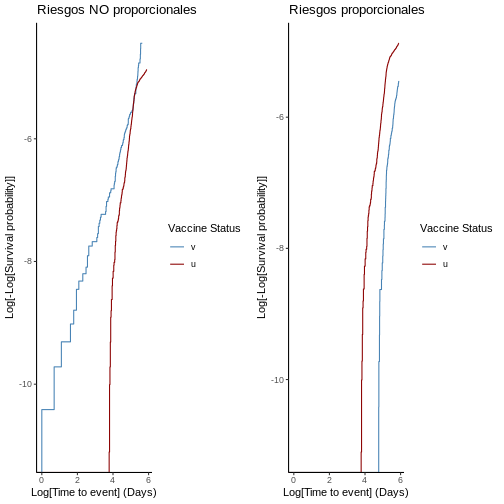
4.5. Estimación de la efectividad vacunal

Modelo de Cox

En todos los estudios observacionales de efectividad vacunal de cohorte se compara el riesgo (o tasa de incidencia) entre los vacunados y no vacunados de desarrollar el desenlace de interés (infección, enfermedad, muerte, etc). La medida de riesgo a utilizar dependerá de las características de la cohorte y puede expresarse en términos de relative risk (RR) o hazard ratio (HR).

En este ejercicio utilizaremos el modelo de regresión de riesgos proporcionales de Cox para estimar el hazar ratio y con esta medida estimar la efectividad mediante

VE= 1-HR

Para estimar la efectividad vacunal en términos de HR, ejecute el siguiente comando en R:

R

coh_eff_noconf(
  data = cohortdata,
  outcome_status_col = "death_status",
  time_to_event_col = "time_to_death",
  status_vacc_col = "vaccine_status")

OUTPUT

      HR HR_low HR_high  V_eff V_eff_low V_eff_high     PH      p_value
1 0.6129 0.5209  0.7211 0.3871    0.2789     0.4791 reject 7.389662e-17

4.6 Cohorte dinámica - Emparejamiento poblacional

El comando anterior arrojó la efectividad vacunal obtenida mediante el model de Cox. Sin embargo, en la columna PH aparece la palabra rejected. Esto significa que pese a que las curvas de ambos grupos son paralelas la evaluación de la hipótesis de riesgos proporcionales haciendo uso del test de Schoenfeld no es satisfactoria. Esto debido a los potenciales sesgos muestrales inducidos por la estrategia de vacunación desplegada sobre la población. Una estrategia para contrarestas dichos sesgos es el emparejamiento dinámico de la población. En la siguiente figura se presenta un esquema de emparejamiento orientado a disminuir los sesgos muestrales.

4.7 Próximos características

Estimador Kaplan-Meier
Curva loglog para evaluación de riesgos proporcionales
Matching dinámico
Censura

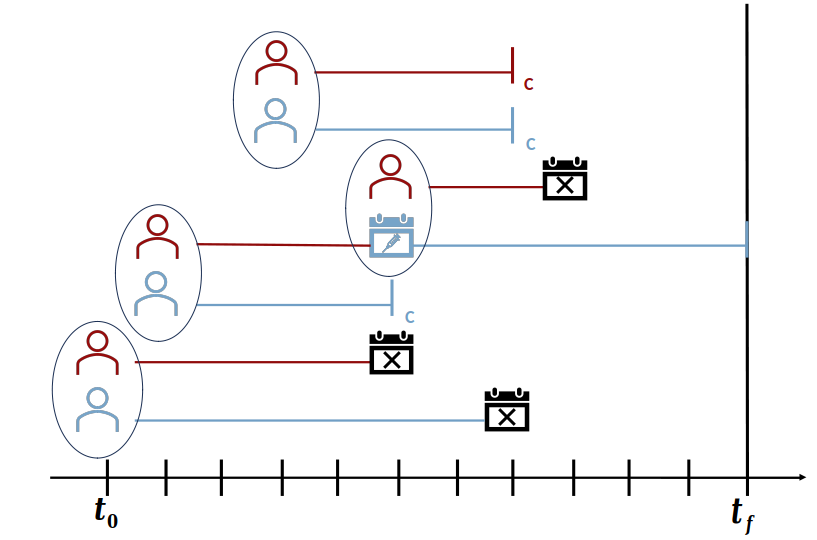
5. Reflexión

En esta sesión se llevó a cabo una estimación básica de la efectividad vacunal mediante un estudio de cohorte, haciendo uso de los estimador Kaplan-Meier y del modelo de Cox. Adicionalmente, se estudió la hipótesis de riesgos proporcionales para los grupos vacunado y no vacunado comparando la construcción de tiempos al evento de forma dinámica y fija. Se observó que pese a que la hipótesis de riesgos proporcionales se corrobora gráficamente en la consrucción de los tiempos al evento con fecha de inicio fija, al evaluar el modelo de riesgos proporcionales de Cox el test de Schoenfeld rechaza esta hipótesis. En general la decisión sobre aceptar o no los resultados es altamente dependiente del acceso a información adicional relevante que permita realizar ajustes a la estimación y capturar dinámicas relevantes.

Reto

Una vez terminado el tutorial proceda a realizar el Reto.

Puntos Clave

Estudiar algunos de los conceptos claves para la implementación de estudios observacionales con diseño de cohortes
Calcular las métricas claves para llevar a cabo un estudio de cohortes
Discutir las ventajas y desventajas de los métodos de estimación no paramétricos y semi-paramétricos de modelos de superviviencia
Aplicar estrategias de emparejamiento de casos y control y discutir su potencial efecto sobre los estudios de cohortes
Estimar la efectividad vacunal haciendo uso de un diseño de cohortes

Sobre este documento

Este documento ha sido diseñado por David Santiago Quevedo para el Curso Internacional: Análisis de Brotes y Modelamiento en Salud Pública, Bogotá 2023. TRACE-LAC/Javeriana.

Contribuciones

David Santiago Quevedo
Santiago Loaiza
Zulma Cucunubá

Model Option	Probability of positive case at age \(a\)	Prior distribution
`constant`	\(\sim binom(n(a,t), P(a,t))\)	\(\lambda\sim uniform(0,2)\)
`tv_normal`	\(\sim binom(n(a,t), P(a,t))\)	\(\lambda\sim normal(\lambda(t-1),\sigma)\\ \lambda(t=1)\sim normal(0,1)\)
`tv_normal_log`	\(\sim binom(n(a,t), P(a,t))\)	\(\lambda\sim normal(log(\lambda(t-1)),\sigma)\\ \lambda(t=1)\sim normal(-6,4)\)

Overview

Questions

Objectives

1. Introducción

2. Agenda

3. Conceptos básicos a desarrollar

4. Paquetes requeridos

R

5. Compartimentos del modelo básico de Zika

6. Parámetros del modelo

Desafío 1

R

7. Ecuaciones del modelo

7.1 Humanos

7.2 Vectores

8. Fórmula para calcular \(R_0\) (Número reproductivo básico)

9. Modelo en R

R

Desafío 2

R

10. Resuelva el Sistema

Desafío 3

R

11. Resultados

Desafío 4

R

11.1 Comportamiento General (Población humana)

R

11.2 Comportamiento General (Población de vectores)

R

11.3 Proporción

R

11.4 La primera epidemia

R

11.5 Algunos aspectos por discutir

11.6 Modele una o más intervenciones de control

Puntos clave

Sobre este documento

Contribuciones

Asuntos legales

Referencias

Overview

Questions

Objectives

Tiempos de ejecución

Introducción

Conceptos básicos a desarrollar

1. Estructura de datos

Preparación previa

Cargue de librerías:

R

Cargue de bases de datos

R

Estructura de los datos

R

OUTPUT

2. CFR

Probabilidad de muerte en los casos reportados (CFR, por Case Fatality Ratio)

R

OUTPUT

Desafío 1

R

R

OUTPUT

Desafío 2

Pista

R

3. Incidencia

3.1. Curva de incidencia diaria

Desafío 3

R

OUTPUT

R

3.2. Cálculo de la incidencia semanal

Desafío 4

R

OUTPUT

4. Tasa de crecimiento

4.1. Modelo log-lineal

Estimación de la tasa de crecimiento mediante un modelo log-lineal

Probabilidad de muerte en los casos reportados (`CFR`, por Case Fatality Ratio)